3

I couldn't find a formal proof for the rule: when a point $(a,b)$ is reflected along $y=x$, it becomes $(b,a)$.

I tried to prove it by sketching out the situation:

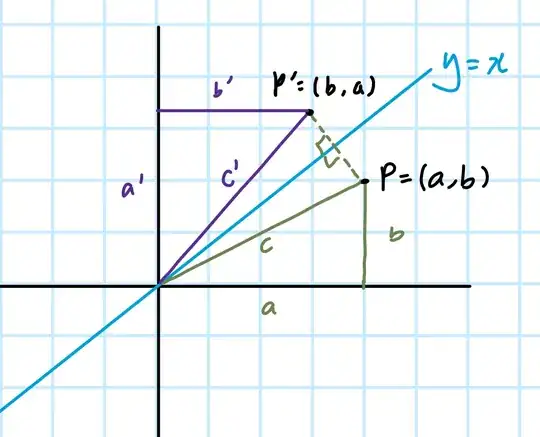
enter image description here

However, I still don't know how to prove that $b'=b, a'=a$.

Furthermore, I just want to make sure, for the following two rules:

  1. Reflection Across Y-Axis. $(x,y)\to(-x,y)$
  2. Reflection Across X-Axis. $(x,y)\to(x,-y)$.

Do they have formal proofs or do we just prove them by visualizing where a point ends up to be on a cartesian plane?

Later
  • 722
  • 2
  • 8
  • 24
Claire
  • 431
  • The proof is made much easier if you are comfortable with vector addition – Ben Grossmann Jul 06 '20 at 22:20
  • For a formal proof, how do you formally define reflection? – Hagen von Eitzen Jul 06 '20 at 22:20
  • 1
    The rules you have for reflections across the x and y axes are correct. – Ben Grossmann Jul 06 '20 at 22:21
  • 1
    I believe this has an answer here. https://math.stackexchange.com/questions/741367/why-does-reflecting-a-point-x-y-about-y-x-result-in-point-y-x – Red Sleuth Jul 06 '20 at 22:22
  • How are you defining a reflection in this context from first principles? Depending on the definition, this won't even need any proof as the properties you mention are merely direct applications of the definitions used. What sort of tools do you have available to you (in terms of mathematical theory)? Reflecting across lines that pass through the origin is covered quite nicely using the language of matrices. See here for instance. – JMoravitz Jul 06 '20 at 22:27
  • @HagenvonEitzen Hi, thanks for commenting! What I mean by reflection is flipping the object about a line of reflection, in which every point is the same distance from the central line – Claire Jul 07 '20 at 02:57

4 Answers4

2

Triangles $(0,0)(1,1)(a,b)$ and $(0,0)(1,1)(b,a)$ are congruent because corresponding sides have equal length (by Pythagoras).

Hagen von Eitzen
  • 374,180
2

To show that $a' = a$ and $b' = b$, consider the triangles formed by $(0,0),(a,0),(0,a)$ and $(0,0),(0,b),(b,0)$.

Using the definition of reflection, conclude that both of these triangles must be isosceles.

Ben Grossmann
  • 225,327
  • Hi, thanks for answering! However, I don't quite understand what you mean by using the definition of reflection. In my interpretation, you are referring to that (a, 0) and (0, a) is same distance away from the central line (y=x). However, since we haven't proved that (a, 0) and (0, a) are reflection points of each other, how can we use that definition? – Claire Jul 06 '20 at 23:12
  • How exactly do you define a reflection across a line? – Ben Grossmann Jul 06 '20 at 23:50
  • I'm thinking of reflection as flipping the object about a line of reflection, in which every point is the same distance from the central line. – Claire Jul 06 '20 at 23:58
  • Hi, if it's not possible to be proven without using vectors, it's okay. I can come back to it after I learn linear algebra. :) – Claire Jul 07 '20 at 00:52
2

Let PP' cut y = x at T. Then T= (t, t) for some t.

T lies on PP' whose slope = -1.

From the above, we get $t = \dfrac{a + b}{2}$

Find the coordinates of P' by recognising T is the midpoint of PP'.

Mick
  • 17,141
  • Hi, thanks for your answer! Could you further explain how you arrive at $$t=\frac{a+b}{2}$$ as I don't quite understand that? – Claire Jul 07 '20 at 04:45
  • 1
    @wl_ Equating the slope (by two points and by -1) to get $\dfrac {b - t}{a - t} = -1$. – Mick Jul 07 '20 at 08:48
0

To find the coordinates of the reflected point $P'$, let us first find the intersection point of the line $y=x$ and the line perpendicular to that line and passing through the point $P=(a,b)$.

As we know, the equation of the line perpendicular to the line $y=x$ and passing through the point $P=(a,b)$ is$$y=-(x-a)+b.$$So, the intersection point can be obtained by solving the following system of equations as follows.$$\begin{cases} y=x \\ y=-(x-a)+b \end{cases} \quad \Rightarrow \quad M=\left ( \frac{a+b}{2}, \frac{a+b}{2} \right ).$$According to the definition of reflection, the point $M$ is the midpoint of the segment $\overline{PP'}$. So the reflected point $P'$ can be obtained by the following vector addition:$$\overrightarrow{OP'}=\overrightarrow{OP}+ 2 \overrightarrow{PM},$$where $O=(0,0)$ is the origin.

So, we need to do some vector algebra as follows.$$\overrightarrow{PM}=\left ( \frac{a+b}{2}, \frac{a+b}{2} \right ) - \left ( \vphantom{\frac{a}{b}} a,b \right )= \left ( \frac{b-a}{2}, \frac{a-b}{2} \right )$$$$\Rightarrow \quad \overrightarrow{OP'}= \left ( \vphantom{\frac{a}{b}} a,b \right )+ 2 \left ( \frac{b-a}{2}, \frac{a-b}{2} \right )=(b,a).$$Thus, the coordinates of the reflected point $P'$ is$$P'=(b,a).$$

Addendum

We can also find the coordinates of the reflected point by equating the distances of the points $P$ and $P'$ from the Point $M$ as follows (Please note that the point $P'$ lies on the line $y=-(x-a)+b$).$$d_{P',M}=d_{P,M}$$$$\Rightarrow \quad \sqrt{\left ( x- \frac{a+b}{2} \right )^2+ \left ( (-x+a+b) - \frac{a+b}{2} \right )^2}= \sqrt{ \left ( a- \frac{a+b}{2} \right )^2 + \left ( b - \frac{a+b}{2} \right )^2}$$$$ \Rightarrow \quad x=a \quad \text{ or } \quad x=b$$ $x=a$ corresponds to the point $P$. Thus, the coordinates of the reflected point $P'$ is$$P'=(b,a).$$

Later
  • 722
  • 2
  • 8
  • 24