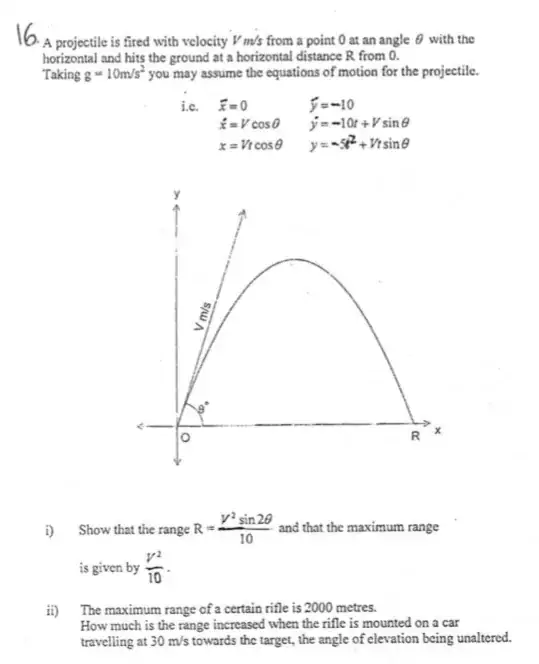
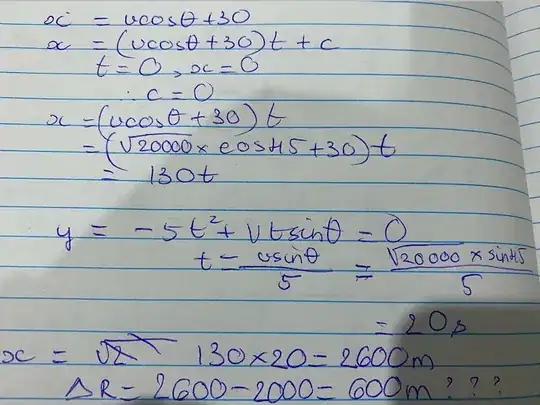Part (i)
Dynamics in $x$-direction: $\ddot{x}=0$, $\dot{x}=V\cos\theta$, $x=Vt\cos\theta$.
Dyanmics in $y$-direction: $\ddot{y}=-10$, $\dot{y}=-10t+V\sin\theta$, $y=-5t^2+Vt\sin\theta$.
(a) Time for projectile to land on the ground: solve $y=0$ for time $t$:
\begin{eqnarray*}
-5t^2+Vt\sin\theta &=&0\\
\end{eqnarray*}
One solution is $t=0$, but that is the initial condition. So, assume $t\neq 0$ and divide by $t$ to get
\begin{eqnarray*}
-5t+V\sin\theta &=&0
\implies t = \frac{1}{5}V\sin\theta
\end{eqnarray*}
This is the time until the projectile lands for any given $\theta$ and $V$.
(b) total horizontal distance traveled before projectile hits ground: use the time until projectile hits ground found in (a) in the expression for $x$ as a function of $t$:
\begin{eqnarray*}
x &=& Vt\cos\theta
= V\Big(\frac{1}{5}V\sin\theta\Big)=\frac{1}{10}V^22\sin\theta\cos\theta = \frac{1}{10}V^2\sin 2\theta
\end{eqnarray*}
This is the horizontal distance travelled up until the projectile hits the ground for any given $\theta$ and $V$.
(c) From (b) we have $R(\theta)=\frac{1}{10}V^2\sin 2\theta$ is the horizontal range as a function of $\theta$ and $V$. The question doesn't state this clearly but they are assuming $V$ is held constant and it is asking which angle maximises the horizontal range. So, differentiate $R(\theta)$ with respect to $\theta$ and set it equal to zero to get
$$
R'(\theta)=\frac{1}{5}V^2\cos 2\theta = 0
$$
Hence, solving gives $2\theta=\frac{\pi}{2}$ and so $\theta=\frac{\pi}{4}$. The maximum range for any $V$ is therefore
$$
R\Big(\frac{\pi}{4}\Big)=\frac{1}{10}V^2\sin\Big(\frac{\pi}{2}\Big)=\frac{1}{10}V^2
$$
Part (ii)
Dynamics in $x$-direction: $\ddot{x}=0$, $\dot{x}=V\cos\theta+30$, $x=Vt\cos\theta+30t$.
Dyanmics in $y$-direction: $\ddot{y}=-10$, $\dot{y}=-10t+V\sin\theta$, $y=-5t^2+Vt\sin\theta$.
From the $x$ dynamics we see that the range is increased by $30t$ no matter what $\theta$ and $V$ are. We know the time until the projectile hits the ground and so we can work out the increase in range for any $\theta$ and $V$:
$$
30t = 30\Big(\frac{1}{5}V\sin\theta\Big)=6V\sin\theta
$$
However, we are told that the maximum range of the rifle, when stationary, is 2000 meters. This means two things (1) the rifle is being fired at an angle of $\frac{\pi}{4}$ so as to maximize range and (2) knowing the range will enable you to find $V$. When the rifle is stationary, the bullet has a maximum range of $\frac{1}{10}V^2$. Hence, we solve
$$
2000=\frac{1}{10}V^2 \implies V=100\sqrt{2}
$$
So, $\theta=\frac{\pi}{4}$ and $V=100\sqrt{2}$. This means the extra range gained by mounting rifle on car is
$$
30t = 30\Big(\frac{1}{5}V\sin\theta\Big)=6V\sin\theta = 6(100\sqrt{2})\sin\Big(\frac{\pi}{4}\Big) = 6(100\sqrt{2})\frac{1}{\sqrt{2}}=600
$$
EDIT
In part (ii), there is some vagueness in the question. It says the maximum range of the rifle is 2000m. It doesn't explicitly say so but I think one has to assume this is the maximum range when the rifle is at rest, which, from part (i), implies that the rifle is being fired at the angle $\frac{\pi}{4}$. Also, the question explicitly states "the angle of elevation being unaltered" whether stationary or moving, so I think we have to assume the angle remains at $\frac{\pi}{4}$ while moving.
However, as pointed out by ab123, one could interpret the problem slightly differently: once moving at 30m/s, one could ask what is the maximum range if one is then allowed to vary the angle. The y-dynamics don't change so we still have the time in the air given by $t=\frac{1}{5}V\sin\theta$ for any $V$ and $\theta$. Now substitute this time into the expression for $x(t)$ to get
\begin{eqnarray*}
x(t) &=& Vt\cos\theta +30 t\\
x\Big(\frac{1}{5}V\sin\theta\Big) &=&
V\Big(\frac{1}{5}V\sin\theta\Big)\cos\theta+30\Big(\frac{1}{5}V\sin\theta\Big)\\
&=&
\frac{1}{10}V^2\sin(2\theta)+6V\sin\theta
\end{eqnarray*}
Note that the extra $6V\sin\theta$ term represents the gain in range due to moving at 30m/s horizontally, and that it depends on $V$ and $\theta$. The time in the air is $t=\frac{1}{5}V\sin\theta$. Intuitively, when we increase the angle from $\frac{\pi}{4}$ to something a little higher we increase the time in the air and hence increase the time during which we can travel horizontally at 30m/s. However, there is an offsetting effect: increasing the angle reduces the x-velocity $V\cos\theta$ due to the rifle elevation. Well, it turns out that there is an optimal angle that maximizes the difference between these two offsetting velocity effects. To find this angle we take the above expression for distance travelled while in the air and maximize with respect to $\theta$, so we take the derivative:
\begin{eqnarray*}
x\Big(\frac{1}{5}V\sin\theta\Big) &=&
\frac{1}{10}V^2\sin(2\theta)+6V\sin\theta\\
\text{ so }0 &=& \frac{d}{d\theta}x\Big(\frac{1}{5}V\sin\theta\Big)=
\frac{d}{d\theta}\frac{1}{10}V^2\sin(2\theta)+6V\sin\theta\\
&=&\frac{1}{5}V^2\cos(2\theta)+6V\cos\theta\\
\end{eqnarray*}
Using $V=100\sqrt{2}$ one can numerically solve for the best angle. I get $0.855$ radians which is $48.99$ degrees, slightly higher than $45$ degrees from the above solution. Putting this angle back into the equation
$$
x\Big(\frac{1}{5}V\sin\theta\Big) =
\frac{1}{10}V^2\sin(2\theta)+6V\sin\theta
$$
one gets that the maximum range is $2620.93$, which is slightly higher than the above solution, and represents and increase of $2620.93-2000=620.93$.
When I originally thought about this problem I thought that, moving or not, the range is always maximised by firing the rifle at $\frac{\pi}{4}$. However, that initial intuition was wrong. Increasing the angle increases the time in the air and hence takes further advantage of the fact that the bullet is moving horizontally at a minimum of 30m/s, no matter what angle of elevation is being used (ignoring the possibility of shooting the rifle in the opposite direction to the direction of motion!). As mentioned, this is offset by a loss of horizontal velocity $V\cos\theta$ but there is an angle that maximizes the difference between gains and losses: 48.99 degrees.