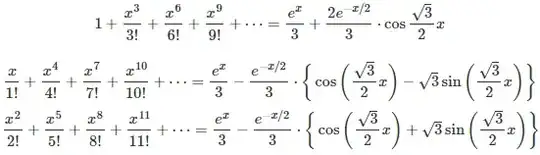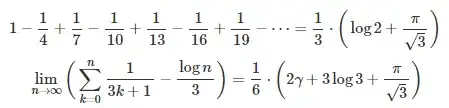3

Does anyone know how to compute $$\displaystyle \lim_{n \to + \infty} \sum_{j=1}^{n}\frac{(-1)^{j+1}}{(3j)!} = \frac{1}{3!} - \frac{1}{6!} + \frac{1}{9!} - \frac{1}{12!} + \ldots ?$$

I guess it may be the Taylor serie of some function applied in some point, since it is similar to $\displaystyle \lim_{n \to + \infty} \sum_{j=1}^{n}\frac{(-1)^{j+1}}{j!} = 1 - \frac{1}{e}$ and $\displaystyle \lim_{n \to + \infty} \sum_{j=1}^{n}\frac{(-1)^{j+1}}{(2j)!} = 1 - \cos(1)$, for example.

3 Answers3

7

Well, the best way to think about this is to know that we have $$e^x = \sum_{n=0}^{\infty}\frac{x^n}{n!}.$$ We are essentially trying to take every third term in the following series, then negate every sixth and then remove the first term: $$e^1 = \frac{1}{0!}+ \frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\ldots.$$ The classic way to do this is to evaluate $e^x$ at various roots of unity and sum them together in a clever way to get the desired answer; for instance, simpler tasks like "take every second term" would be $\frac{1}2\left(e^{1}+e^{-1}\right)$. This is because the averages of $\frac{1}2(1^n + (-1)^n)$ is a sequence that is $0$ when $n$ is odd and $1$ when $n$ is even - so looking at power series gives that that sum is the even terms of the given sum.

Similarly, one can see that if $\gamma=e^{2\pi i/3}$ is a third root of unity, then the average $\frac{1}3(1+\gamma^n+\gamma^{2n})$ is $0$ whenever $n$ is not divisible by $3$ and $1$ otherwise. This leads us to see that $\frac{1}3(e^{1}+e^{\gamma}+e^{\gamma^2})$ is the sum of every third term in the series, because every other $x^n$ term cancels across the three different sums.

A little bit more finesse gives that the number you desire is given by negating the exponents (to get the desired alternation of sign), then subtracting the whole thing from $1$ to get the first sign correct and cancel the first term. Thus, your sum evaluates to $$1-\frac{1}3\left(e^{-1}+e^{-\gamma}+e^{-\gamma^2}\right).$$ We can then write this in real terms by evaluating $\gamma = \frac{-1}2 + \frac{\sqrt{3}}2 i$ and noting that $e^{a+bi}+e^{a-bi}=2e^a\cos(b)$. This gives the sum as $$1-\frac{1}3\left(\frac{1}e+2e^{1/2}\cos\left(\frac{\sqrt{3}}{2}\right)\right)$$ which agrees well with what you get when you evaluate the sum numerically.

Travis Willse
  • 99,363
Milo Brandt
  • 60,888
2

Recall $$e^x=\sum_{j=0}^\infty \frac{x^j}{j!}.$$ Let $\omega=e^\frac{2i\pi}{6}$. Notice that $$\omega^k+\left(\frac1{\omega}\right)^k+(-1)^k=\left\{\begin{array}{lr} 0, & \text{for } 3\nmid j\\ -3, & \text{for } 3\mid j,6\nmid j\\ 3, & \text{for } 6\mid j \end{array}\right\}.$$ Therefore, $$1-\frac13\left(\exp(\omega)+\exp\left(\frac1{\omega}\right)+\exp(-1)\right)$$ gives your desired sum. $\blacksquare$

ViHdzP
  • 4,582
  • 2
  • 18
  • 44
  • 1
    I don't think this is right; $\omega^k + \omega^{-k}$ is never $0$ - for $k=0,1,2,3$, the values are $2,1,-1,-2$. Note that $\omega = \frac{1}2 + \frac{\sqrt{3}}2i$ and $\omega+\omega^{-1}$ is clearly not zero as this answer claims. – Milo Brandt Dec 23 '19 at 00:17
  • @MiloBrandt You’re right, I made some mistakes. Let me see if this is quickly fixable, or otherwise I’ll delete this. – ViHdzP Dec 23 '19 at 00:22
  • @MiloBrandt This should now be fixed. I forgot a term and had some sign errors at the end. This answer now agrees with yours. – ViHdzP Dec 23 '19 at 00:38
2

More similar results, obtained using the same kind of reasoning:

enter image description here

Also:

enter image description here

See proof for these results in one of my articles, here.

Vincent Granville
  • 3,605