I have a rectangular container with sides A,B. I have a second rectangle with sides C,??
Side ?? should be the largest length possible while still remaining inside rectangle A,B. I need to create and excel formula to solve for this but cannot figure out the math. I found one post on this website which i thought might be the answer but it started talking about Newton's Method and i can't seem to figure it out.
Given a large rectangle with sides $A$ and $B$, we want to maximize the side(call it "x") of an inscribed rectangle with given side $c$. There are at least 2 and probably many more ways to solve this, but as far as I know, they are all going to be finished numerically, which precludes finding a single explicit equation which can be used in an Excel formula. However, it probably could be done in Excel, using either Newton's method or a similar Excel equation solver. I am not going to show an Excel solution.
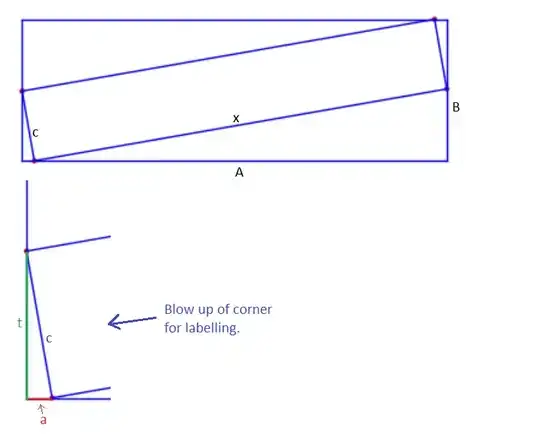
One simple(ish) method is the following. Let's look at the diagram. We see two small right triangles and two larger right triangles. The small ones have a Pathagoras eq of $$a^2+t^2=c^2 \tag{1}$$. The large ones are $$(A-a)^2+(B-t)^2=x^2 \tag{2}$$ In this setup, we basically have 3 unknowns, "a", "t", and "x". The third equation that will be used is one for the area of the whole figure. That is, equate the sum of all the pieces to $A\cdot B$, the whole area. A critical insight is to see that the two small triangles are identical as are the two large triangles. Therefore the third equation is $$A\cdot B= t\cdot a+(A-a)(B-t)+c\cdot x \tag{3}$$
To solve, we begin by solving the first equation for "t". $$t=\pm \sqrt{c^2-a^2}$$ For this problem, with positive real line lengths, "t" will always be the positive square root. (I'm not 100% certain of that! Haven't tried cases where $c>min(A,B)$.) Substitute in for $t$ in the second equation. $$(A-a)^2+(B-\sqrt{c^2-a^2})^2=x^2$$, then solve for x. $$x=\sqrt{(A-a)^2+(B-\sqrt{c^2-a^2})^2} \tag{4}$$ Now substitute in for both $x$ and $t$ in the third equation. $$A\cdot B= \sqrt{c^2-a^2}\cdot a+(A-a)(B-\sqrt{c^2-a^2})+c\cdot \sqrt{(A-a)^2+(B-\sqrt{c^2-a^2})^2}$$ The problem is how to solve this for "a" and the usual answer can be with Newton's method. Let $$f(a) = \sqrt{c^2-a^2}\cdot a+(A-a)(B-\sqrt{c^2-a^2})+c\cdot \sqrt{(A-a)^2+(B-\sqrt{c^2-a^2})^2}-A\cdot B$$ then the derivative is $$f'(a)=\frac{{\left(A - a\right)} a}{\sqrt{-a^{2} + c^{2}}} - \frac{a^{2}}{\sqrt{-a^{2} + c^{2}}} + \frac{{\left(\frac{{\left(B - \sqrt{-a^{2} + c^{2}}\right)} a}{\sqrt{-a^{2} + c^{2}}} - A + a\right)} c}{\sqrt{{\left(A - a\right)}^{2} + {\left(B - \sqrt{-a^{2} + c^{2}}\right)}^{2}}} - B + 2 \, \sqrt{-a^{2} + c^{2}}$$ Now if you plug in numbers for A, B, and c, then we can guess a value for "a" and Newton's method will improve the guess. Then you guess again and again until the value quits changing for the number of decimals that you can display. $$a_{new}=a_{guess}-\frac{f(a_{guess})}{f'(a_{guess})}$$ That derivative was the (ish) part of it's simple. (This is 7th grade math, with calculus.)
If you want to see if you have coded one correctly, let $A=4$, $B=3$ and $c=1$. Then after a few iterations (about 7), ('a =', 0.5262147424733005) ('t =', 0.8503517182929414). Then you can calculate x=4.085115879685171 from eq 4.
That being said i am wondering how you know where to start your a-guess? with your example i started as .5 and every number i plugged in made the next guess smaller and smaller instead of larger. I also started with .75 and it took way more that 7 iterations to zero in on the answer.
– IHamilton Dec 10 '19 at 17:00Your small rectangle is rotated by some angle $\theta$ relative to the big one. $C$ is the hypoteneuse of a little right triangle whose legs are $C \cos\theta$ (vertical) and $C \sin\theta$ (horizontal). Note that, for the small rectangle to fit,
$$ \tan\theta = \frac{B - C \cos\theta}{A - C\sin\theta} $$
You'll probably have to solve this numerically. Then, if the length you seek is $D$,
$$ D \cos\theta = A - C\sin\theta $$
