Many of the older (circa 1850-1925) books on projective geometry discuss the geometry of two conics. For example, points of intersection, common chords, common tangents, etc. A self-polar triangle for a given conic is a triangle whose edges are the polars of its vertices, and whose vertices are the poles of its edges. It is not unique, but the common self-polar triangle of two given conics, if it exists, is unique.
My question is whether there is a ruler and compass construction for the common self-polar triangle of two non-intersecting non-nested ellipses.
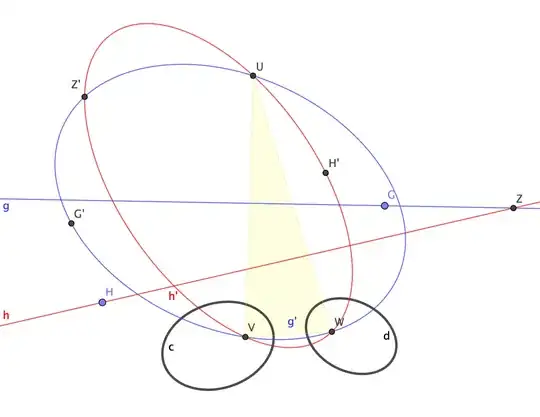
The books show how to determine the common self-polar triangle $\triangle{UVW}$ as in the following diagram.
Start with the two conics $c$ and $d$. For any point $X$, its reciprocal $X'$ is the intersection of the polars of $X$ with respect to $c$ and $d$. The reciprocal $l'$ of a line $l$ is the locus of the reciprocals $P'$ of points $P$ on $l$. It turns out to be a conic, so we call it the reciprocal conic of $l$.
Shown in the diagram are the lines $g,h$ and their reciprocal conics $g',h'$. These conics intersect at $Z'$, the reciprocal of the intersection $Z$ of the two lines. The other three intersection points - $U,V,W$ - are the vertices of the common self-polar triangle. Also shown are some reciprocal pairs $G,G'$ and $H,H'$.
The problem, which none of the books address, is that in general it is not possible to synthetically construct the intersection of two conics that are given by, say, 5 points each. It is possible to do so if two or three of the intersection points are known, but one known intersection point is not enough.
On the other hand, the setup is rich enough that there may be a ruler/compass construction. As the lines $l$ vary, their conjugate conics always go through $U,V,W$ ($Z'$ will vary). Or there may be a synthetic construction of $U,V,W$ that goes through another route. Or the books may be skipping over this step because they consider it to be obvious. Or the construction may be impossible using ruler and compass.
Examples of the construction given in the books are Russell, Pickford, and Hatton