How to check the convexity of this function?

Question

I have a function $g(x,y,\alpha)$ that for $g(x,y,\alpha)=0$ defines a closed surface of $x$ and $y$. Depending on the varable $\alpha$ the shape of the surface changes, see the figure below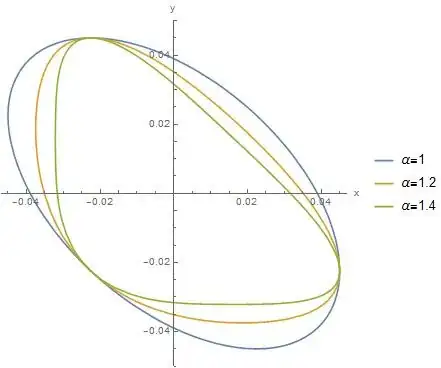$g$ on the parameter $\alpha$">.

As you can see in the figure, upon increasing the parameter $\alpha$, the shape of the closed surface changes and corners are created. I would like to find the critical value of $\alpha$ for which the closed surface $g(x,y,\alpha)=0$ is not convex anymore.

The function $g$ is a bit complex but I provide its expression just in case it is needed

$g=-0.049(\frac{1}{1+\alpha^3})^\frac{1}{3}+((x^2 +x y + y^2)^\frac{3}{2}+\frac{3\sqrt{3} x y (x+y)(-1+\alpha^3)}{2(1+\alpha^3)})^\frac{1}{3}$.

$\textbf{What I did so far:}$

I know that for the function $g(x,y,\alpha)$ to be convex its Hessian matrix should be positive semi-definite. So I calculated the Hessian as follows

$\mathbf{H}=\begin{pmatrix} \frac{\displaystyle \partial^2 g}{\displaystyle \partial x^2} & \frac{\displaystyle\partial^2 g}{\displaystyle \partial x \partial y} \\ \frac{\displaystyle \partial^2 g}{\displaystyle \partial y \partial x} & \frac{\displaystyle \partial^2 g}{\displaystyle \partial y^2} \end{pmatrix}$.

In order to ensure the positive semi-definiteness of the Hessian $\mathbf{H}$, its eigenvalues must be positive. Thus, it should satisfy the following conditions:

1. $\det(\mathbf{H})>0$.

2. $\frac{\displaystyle \partial^2 g}{\displaystyle \partial x^2}>0$.

However, after calculating I understood that $\det(\mathbf{H})$ is zero for every $\alpha$ and also $\frac{\displaystyle \partial^2 g}{\displaystyle \partial x^2}$ is too complex. Therefore I couldn't determine the positive semi-definiteness of $\mathbf{H}$ with this procedure.

I would like to know if I am on the right path for the determination of the critical value of $\alpha$ for which the surface $g$ is not convex. If yes, then how can I continue.

Answer 1

Switch to polar coordinates $x = r \cos(\theta)$, $y=r \sin(\theta)$, and you can explicitly parametrize your curve as $r = R(\theta)$. The criterion for a smooth polar curve to be convex is $r^2 + 2 (r')^2 - r r'' \ge 0$ for all $\theta$, which is rather a mess here. Numerically minimizing $\alpha$ subject to the constraint $R^2 + 2 (R')^2 - R R'' = 0$, I find that the critical $\alpha$ is approximately $1.44224957028754$.

Answer 2

I would introduce $z=-x-y$ so it is a shape on the plane $x+y+z=0$. Then there are $(r,\theta)$ with $$x=r\cos\theta\\y=r\cos(\theta+2\pi/3)\\ z=r\cos(\theta-2\pi/3)$$ Then the equation is $$(x^2+y^2+z^2)^{3/2}-cxyz=d\\ r^3(1-p\cos3\theta)=q$$ You can work out $p$ and $q$ in terms of $\alpha$.
Then $x=r\cos\theta$ so $$x^3=\frac{q\cos^3\theta}{1-p\cos3\theta}$$ The shape is convex if $x$ has a local maximum at $\theta=0$ Find the value of $p$ for which the second derivative $d^2(1/x^3)/d\theta^2=0$.