108

This is a prime-removal algorithm I made, which may appear to be quite complex so I will start with an example. @Max has since added this sequence to OEIS, number A332198.

The process goes as follows:

  • Start with the first prime number, $$S(1)=2.$$

  • From $2$, add the next prime number $3$ to get $$S(2)=2+3=5.$$ There are no non-trivial factors, so we move on.

  • From $2+3$, add the next prime number $5$ to get $$S(3)=2+3+5=10.$$ Since $10=2\times5$ and these two numbers appear in the sum, we remove $2$ and $5$.
    We are left with $3$.

  • From $3$, add the next prime number $5$ to get $$S(4)=3+5=8.$$ Now $8=2\times2\times2$, but $2$ does not appear in the sum, so we move on.

  • From $3+5$, add the next prime number $7$ to get $$S(5)=3+5+7=15.$$ Since $15=3\times5$ and these two numbers appear in the sum, we remove $3$ and $5$.
    We are left with $7$.

  • (and so on)

So essentially, we keep on adding consecutive prime numbers until we reach a sum whose prime factorisation contains some of those primes. We remove those primes and start the process once again. Great, except...

There is one more rule that needs to be added. If we continue doing this, we soon find ourselves in a rather strange scenario.

  • (and so on) a continuation:

  • From $37+47+59+\cdots+241+251+257$, add the next prime number $263$ to get $$S(57)=37+47+59+\cdots+251+257+263=5918.$$ Now $5918=2\times11\times269$, but neither of the three primes appear in the sum, so we move on.

  • From $37+47+59+\cdots+251+257+263$, add the next prime number $269$ to get $$S(58)=37+47+59+\cdots+251+257+263+269=6187.$$ Since $6187=23\times269$ and $269$ appears in the sum, we remove $269$.
    We are left with $37+47+59+\cdots+251+257+263$.

This is a cycle! The sequence of $263$ and $269$ will continue forever, if we don't add another rule to this process. Therefore, I call $269$ a cyclic prime, and I propose this new rule.

  • From $37+47+59+\cdots+251+257+263$, add the next non-cyclic prime number $271$ to get $$S(59)=37+47+59+\cdots+251+257+263+271=6189.$$ Now $6189=2\times2063$ and these two numbers do not appear in the sum, so we move on.

I do not know whether there are any dicyclic primes; that is, primes that are still cyclic after more than one iteration.

Questions

  1. Will every prime number in the sum eventually be removed? If not, which prime numbers will remain in the sum forever?

It appears to be true. From this Python program by @EuxhenH, we see that all primes up to $16903$ are eliminated at some point before overflow. The table linked shows how long it takes ($N$ iterations) for the smallest prime $P$ in the sum to be removed. It appears that $P$ increases as $N$ increases despite significant fluctuation.

  1. Follow-up: What is the asymptotic growth of $N(P)$? For instance, does it admit a $\log$ or $\log\log$ increase?

  2. Are there infinitely many cyclic prime numbers?

As of writing, the only known cyclic prime numbers are $269$ and $94793$.

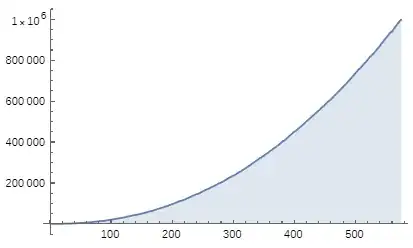
Using @Max's PARI/GP program, I plotted $S(n)$ for $n\le575$ enter image description here

which should grow like $Cx^a\log^bx$.

Note that this sequence, by definition, is bounded above by $$\sum_{i\le n}p_i\sim\frac12n^2\log n.$$ Indeed, when $a=2$ and $b=1$, Mathematica gives an optimal value of $C\approx0.4716$. However, the residual plot suggests there is perhaps a better asymptotic.

ə̷̶̸͇̘̜́̍͗̂̄︣͟
  • 27,005
  • 2
    How can you possibly know which next prime is non-cyclic? I don't think this part is computable, unless there is some hidden proof or trick. – EuxhenH Jul 08 '19 at 12:31
  • 1
    @EuxhenH If $\require{cancel}p_{n+1},\cancel{\Bigg\vert},\sum_{p_i\in\text{sum}} p_i$ where $\text{sum}$ is the existing sum, then we know that the next prime cannot be cyclic since the factors of $\text{sum}$ do not include the next prime. – ə̷̶̸͇̘̜́̍͗̂̄︣͟ Jul 08 '19 at 12:37
  • But at the same time there are primes which divide the sum and yet are not cyclic. As in your example, $5$ divides $2+3$, but $5$ is not cyclic. Let me add the condition that $p_{n+1}$ is cyclic if it divides $\sum_{p_i\in\text{sum}}p_i$ and such that none of the factors of $\frac{\sum_{p_i\in\text{sum}}p_i}{p_{n+1}}$ are present in the list of factors.

    Note: This may be incorrect, I didn't prove it, but it is just a guess.

     – EuxhenH Jul 08 '19 at 13:13
  • a cyclic prime in this case will have pairs of primes cancel mod that prime, or at least subsets. –  Jul 11 '19 at 16:14
  • The prime $p$ is removed if $S\ne p$ and $S=0 \pmod p$? Where $S$ is the sum so far. I wonder if the sum has the same properties (every prime is eventually removed?) if instead of $0$, we choose some other remainder $m$ as "removing condition"? Because you don't allow cycles of remainders by not allowing cycles, I think every remainder modulo $p$ will be achieved at some step and remove $p$ regardless of $m$ eventually, given any current smallest prime $p$. If a counterexample exists, a non-cyclical (paternless, "irrational") sequence of remainders must be achieved for all following primes? – Vepir Aug 20 '19 at 11:45
  • 2
    I have a probabilistic interpretation for the first question, this is not a demonstration, just an intuition on why this might be true.

    Take a prime p in the sum, by dirichlet theorem for any 0<k<p there are infinitely many primes that are congruent to k mod p, as a result if you consider that you pick your next prime at random, you have a positive probability that the sum will be a multiple of p and so almost surely, you end up on a multiple of p.

    In our case, the next prime we add isn't chosen at random so I'll say it again, this is not a proof, just an intuition.

     – Statistic Dean Aug 20 '19 at 12:06
  • 2
    Please explain what next prime means - next to what? If it's next to the prime added last, then why do you care whether $269$ was removed or not? (as we simply add $271$, then $277$ and so on - no matter what) Or, would it be equivalent to says that to the sum $S$ we add the smallest prime that is larger than the terms of $S$ and that does not divide $S$? – Max Alekseyev Oct 08 '19 at 15:02
  • @Max they showed the factorization has the prime just eliminated and no others ( or certain subsets but I digress) which would be next in line after elimination from S . –  Dec 03 '19 at 03:33
  • @TheSimpliFire Can one say that this idea is conjecture ? I feel like it is conjecture and it is really very much interesting ... I hope that you go on discovering it more and find great results...like you have done today ... you added new details...when I become stronger at mathematics I would also think about this great idea and if I come to good result I will share it with you as answer in this question. – Mahmoud albahar May 04 '21 at 15:00

1 Answers1

8

I have no proof so far but also written a program that checked that the only cyclic primes among the first $10^5$ steps are $p = 269$ in $S(58) = 6187$, and $p = 94 793$ in $S(9141) = 377 844 898$, where I call $S(n)$ the value of the sum at step $n$ (after adding the "next larger prime", not considering the removal of terms as a step, with $S(1) = 2$ which can be seen as result of adding $2$ to the empty sum $S(0)$).

FWIW, I get \begin{align}S(1000) &= 3\,362\,713\\S(2000) &= 14\,797\,503\\S(5000) &= 105\,157\,142\\S(10\,000) &= 456\,622\,646\\S(20\,000) &= 1\,979\,852\,987\\S(50\,000) &= 13\,618\,461\,808\\S(10^5) &= 58\,316\,786\,321.\end{align}

The smallest prime in the sum at these points is \begin{align}p(1000) &= 457\\p(2000) &= 509\\p(5000) &= 1451\\p(10\,000) &= 2281\\p(20\,000) &= 4129\\p(50\,000) &= 10\,631\\p(77\,000) &= p(10^5) = 16\,903.\end{align}

To be precise, my program considers a prime cyclic if it would give twice the same result, $\widehat S(n+1) = S(n)$, if it were used, which is then however avoided by using the next larger prime. I agree that this may not be the conceptually most satisfying definition... On the other hand, $p_{k+1}\mid\sum p_i$ isn't complete either (as mentioned in a comment), because depending on the smaller primes removed at that step or the next one, this does not necessarily give a loop. [However, if I'm not wrong, it's excluded that the next smaller prime is a factor of the sum at the same time as the largest prime $p_{k+1}$, because the sum is at most $\sim p_{k+1}^2/2 < p_{k}\cdot p_{k+1}$.]

The experimental results seem to confirm that eventually all primes will be removed. I agree with the heuristic argument that, if there's no particular modular restriction on the sum, then any prime factor will eventually occur (even infinitely often), and thus be removed from the sum. Given the "sequential" way of adding one prime after the other to the sum, there appears indeed no reason that from some point on, a particular prime factor should never occur again. This would yield the required result, but again, it's not a proof.

PS: I proposed the sequence $S(n)$ as oeis.org/A332198, where my program can be found.

ə̷̶̸͇̘̜́̍͗̂̄︣͟
  • 27,005
Max
  • 439