0

(1 + 1/n)^n approximates e^1.

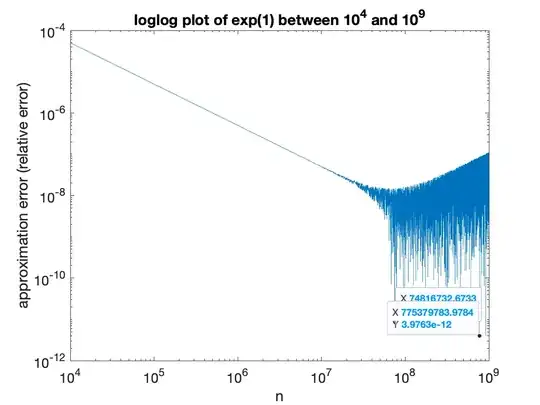
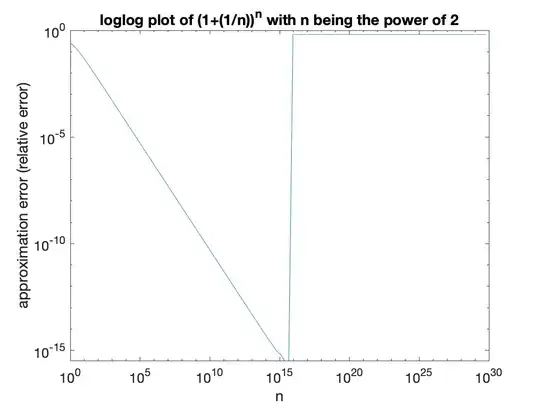
Case 1: When n is equally spaced between 10^4 and 10^9 with 10000 different numbers, linspace(10.^4, 10.^9, 10000) (Done in Matlab). Here's the graph: enter image description here

Case 2: When n is in power of 2, i.e. 2^0, 2^1, 2^2..... Here's the graph: enter image description here

I just started to learn numerical analysis, so this really puzzles me.

I am wondering what's the logic behind it. I understand that 1 + 1/n can't be represented correctly in floating point number, so when calculating there would be error like this: 1 + 1/n + δ. But why is that the 2 graphs are so different though? Case 1, the graph fluctuates drastically between 10^8 to 10^9. But in case 2, from 10^8 to 10^9, it's a straight line. And starting from 10^15, the round-off errors are exponentially increasing..... why?

I should note that the calculation is done in 16 digits of precision. In 32 digits of precision, both cases produce straight line. But I would like to know why is that in 16 digits of precision, things are so different.

Joshua Leung
  • 555
  • 1
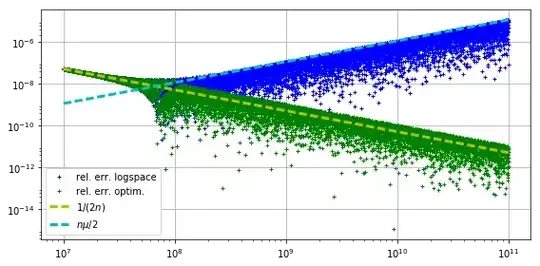
    The jump that you see in the powers of $2$ case is due to $1/n$ becoming smaller than the machine epsilon, which for double precision floating point numbers is around 2.220446049250313e-16. That is why for $n$ somewhat larger than $10^6$ the $1+1/n$ becomes just $1$. – logarithm May 24 '19 at 23:01
  • @logarithm do you mean larger than 10^6 or 10^16?? – Joshua Leung May 24 '19 at 23:05
  • Yes, the latter, of course. – logarithm May 24 '19 at 23:06
  • @logarithm does that mean when a floating point number is less than machine epsilon, it will become 0 because of overflow? – Joshua Leung May 24 '19 at 23:16
  • In the second case there are no rounding errors, as $1+1/n$ is exactly representable in the double precision floating point format. Meaning that the error only has the main term $-1/(2n)$ which you see as the slope $-1$ line. – Lutz Lehmann May 25 '19 at 06:32
  • No, machine epsilon is much larger than the smallest positive number that can be represented. The smallest normal number should be around $10^{-308}$ and the smallest subnormal around $10^{-324}$. What happens with the machine epsilon $\epsilon$ is that $1+\epsilon>1$ but for $\epsilon>a\geq0$ you will have $1+a=1$. – logarithm May 25 '19 at 13:29
  • This is a quick good read. – logarithm May 25 '19 at 13:32

1 Answers1

1

The $δ$ occurs from rounding $1+\frac1n$ to the mantissa length. As such, $2^{52}δ$ is the distance of $\frac{2^{52}}n$ to the next integer, thus is a number between $\pm2^{-53}$. With $\mu=2^{-52}$ the machine number $=$ distance between floating point numbers in $[1,2]$, this can be summarized as $|δ|\le\fracμ2$.

This then leads to the main error contributions $-\frac1{2n}$ and $nδ$ in the computed result as in this answer to your previous question.

Now one can make out several special cases

  • $δ=0$ if $1+1/n$ can be expressed exactly as binary number, requiring $n=2^k$, $k\le 52$. Then the relative error is, for $k>26$, also exactly $-\frac1{2n}$, leading to the straight line in the second loglog plot.

  • $δ>0$ in such a way that $1+\frac1n+δ=e^{\frac1n}$ exactly or with a very small error. Then $(1+\frac1n+δ)^n=e$ also either exactly or with an unusually small error. Using $\frac1n+δ=2^{-52}m$ to get $m=[\frac{2^{52}}n]$ and $n=\lceil\frac1{\ln(1+2^{-52}m)}\rceil$ in an iteration to get such special $n$ from a given start point. Just one such iteration starting from a geometric sampling of $10^4+1$ numbers between $10^7$ and $10^{11}$ gives the following plot comparing the original error and the error of the optimized near-by integer.

    enter image description here

    Exceptionally small errors found within this plot are at

    n=  81959632 : err[n]= 8.30669e-13, 1/(2n)= 6.10056e-09
n=  92214671 : err[n]= 4.14113e-12, 1/(2n)= 5.42213e-09
n= 269153484 : err[n]= 9.54792e-14, 1/(2n)= 1.85768e-09
n= 374282918 : err[n]= 7.42517e-13, 1/(2n)= 1.33589e-09
n=2664404105 : err[n]= 4.04121e-14, 1/(2n)= 1.87659e-10
n=9323952572 : err[n]= 1.11022e-15, 1/(2n)= 5.36253e-11

  • As for $n>2^{26}$ one gets $m<2^{26}$, in the floating point calculation only the first two terms of the logarithm series expansion are effective, thus $\frac1{\ln(1+2^{-52}m)}\approx\frac{2^{52}}{m-2^{-53}m^2}\approx\frac{2^{52}}m+0.5+2^{-54}m$, so that one can simplify the iteration to $m=[\frac{2^{52}}{n}]$, $n=\lceil 0.5+\frac{2^{52}}m\rceil$, giving a similar plot.

    As can be seen, this "optimization" for the most part gives samples where $|δ|$ is close to $\frac1{2n^2}$ or smaller, so that the theoretical error terms dominate the floating point errors, the relative errors accumulate closely around the line $\frac1{2n}$.

Lutz Lehmann
  • 126,666