Why does a constant positive Gaussian curvature imply a sphere?

Question

The Gaussian curvature value $G$ is the product of the two principal curvatures, which are the largest, $\kappa_1$, and the smallest (most downwards-curving), $\kappa_2$, normal curvatures through a point): $$G=\kappa_1\kappa_2$$

For a mountain top as well as a valley, we have a positive $G>0$, because both principle curvatures are either upwards or downwards. The same is the case for a sphere (rightmost figure below). A saddle point, on the other hand, will have negative $G<0$ (leftmost figure). And a flat surface as well as a surface which is 'flat' in one dimension, such as a cylinder (middle figure), will have $G=0$.

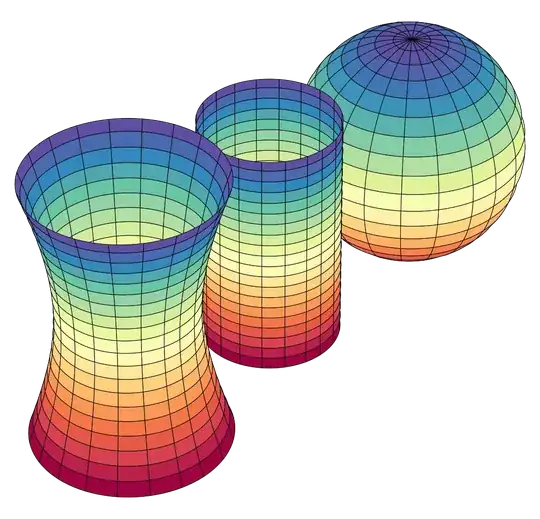^{Image from Wikipedia}

My question is regarding a specific claim from the article on Gaussian curvatures on Wikipedia ("Relation to geometries" headline, middle sentence):

When a surface has a constant zero Gaussian curvature, then it is a developable surface and the geometry of the surface is Euclidean geometry.

When a surface has a constant positive Gaussian curvature, then it is a sphere and the geometry of the surface is spherical geometry.

When a surface has a constant negative Gaussian curvature, then it is a pseudospherical surface and the geometry of the surface is hyperbolic geometry.

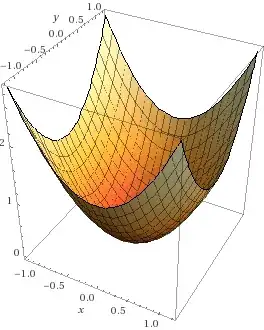
These three sentences seemingly cover all types of surfaces. But the middle sentence (I have emphasized it) tells that for a positive $G>0$, the curvature is a sphere. How can that be true? Don't many mountain top surfaces have a positive $G>0$ all the way down from the top to forever? Such as the function $f=x^2+y^2$ (graph below)?

^{from WolframAlpha}

Answer 1

This is a non-trivial fact. It is possible to create surfaces of revolution of the form

$$(\phi(v) \cos(u), \phi(v) \sin(u), \psi(v)),\quad \phi \ne 0$$

If $v$ is arc length we have $(\phi')^2 + (\psi')^2 = 1$. Having constant Gaussian curvature, K, then implies $\phi''+K\phi = 0$ and $\psi = \int \sqrt{1-(\psi')^2}\ dv$.

With $K=1$ and the curve intersection the X-Y plane perpendicularly we have

$$\phi(v) = C \cos v,\quad \psi(v) = \int_0^v \sqrt{1-C^2 \sin^2 v}\ dv.$$

So $\psi(v)$ is an Incomplete elliptic integral of the second kind. (Reference Do Carmo)

Now these surfaces have constant positive Gaussian curvature, if $C=1$, it gives a sphere, if $C\ne 1$, you have surface which have two singular points on the rotation axis. Examples of such surfaces can be seen at Wolfram demonstrations.

One of the comments above points to a looseness in Wikipedia's statement. The sphere is the only compact, simply-connected, Riemannian surface of constant positive curvature. The above examples, either fails to be compact if we exclude the singular points, or if they are left it fails to be smooth, hence not Riemannian.

Wikipedia does give a hint to a proof of the fact, it references the Liebmann's theorem (1900), and a brief comment that

A standard proof uses Hilbert's lemma that non-umbilical points of extreme principal curvature have non-positive Gaussian curvature.

This may have come from Hilbert and Cohn Vossen (p228). They first show that surface of constant positive Gaussian curvature, without boundary or singularities, must be a closed surface. Apart from the sphere there are no surfaces where both principal curvatures are constant. So we just need to consider cases like the above where the two principle curvatures vary, but their products are constant. As the surface is closed there must be a point where one of the principle curvature obtains its maximum value. But it can be proved analytically that such points can't exist, except on the boundary, on surfaces with constant positive Gaussian curvature.

do Carmo, Manfredo Perdigão, Differential geometry of curves and surfaces. Mineola, NY: Dover Publications (ISBN 978-0-486-80699-0/pbk). xvi, 510 p. (2016). ZBL1352.53002.

Answer 2

^{A simple comment by @user10354138 gave the answer. I simply didn't care enough for the meaning of constant. It is now clear for me, and I will here answer and close the question.}

As pointed out in the comments, the keyword here is constant positive Gaussian curvature. While a mountain top surface such as $f=x^2+y^2$ has a positive Gaussian curvature $G$ at all points, the value of $G$ changes and becomes less positive for points farther from the stationary point (the peak), because the curvatures widen and become "less sharp" as the surface broadens out away from its peak.

A constant $G$ requires the same type of curvature at any point. The same shape as seen from every point. That is clearly only the case for a sphere. Wikipedia is right.