how to find the point obtained by reflecting over a line?

Question

Given the point $A=(-2,6)$ and the line $y=2x$,what are the coordinates of the point B obtained by reflecting A over the line $y=2x$ ?

Can someone teach me how to solve this question please?

Answer 1

$B$ is going to lie on the line that goes through the point A and is perpendicular to $y=2x$. The slope of the line that's perpendicular to a given line is the negative reciprocal of the slope of that given line. So, we have a slope and a point. That's enough information to find the equation of that perpendicular line:

$$y=-\frac{1}{2}x+5$$

Next, find the point where those two lines intersect:

$$-\frac{1}{2}x+5=2x\implies (2,4)$$

The x-coordinate of $B$ is going to be the same distance away from the point $x=2$ as $A$. $A$ is 4 units away from $x=2$. Therefore, the x-coordinate of $B$ is $2+4=6$. The exact same argument goes for the y-coordinate of $B$. The y-coordinate of $A$, which is $6$, is $2$ units away from $4$. This means that the y-coordinate of $B$ is going to be $4-2=2$. So, $(6,2)$ is the point $B$ you're looking for.

Answer 2

Note that AB has a gradient of $-\frac{1}{2}$, and that AB, which is $y=-\frac{1}{2}x+c$ intersects $y=2x$ at the midpoint of AB.

Sub $(-2,6)$ into $y=-\frac{1}{2}x+c$, and solving, $c=5$.

Equate the two equations.

$-\frac{1}{2}x+5=2x$

Coordinates of midpoint of AB: $x=2$, $y=4$

Coordinates of B: $x=2+2+2=6$, $y=4-(6-4)=2$

Answer 3

For reflection there is a reflecting surface (in our case the line $y=2x$) and an object whose reflection is obtained about the surface. In this case the object is the point $A(-2,6)$. Now, for reflection there are two things, the distance of the point from the surface is the same as the distance of the reflection from the surface. And the second thing is that the line joining the point and the reflection is normal to the reflecting surface.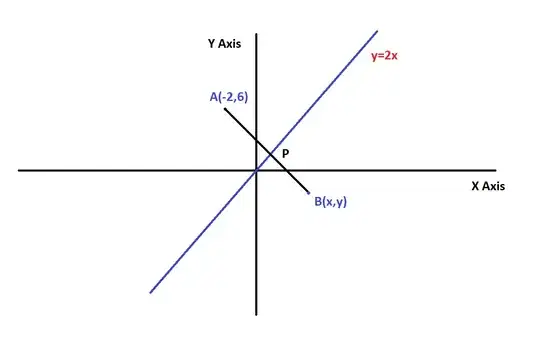

Now, let us say the point $A(-2,6)$ has a reflection $B(x,y)$ on the line $y=2x$.From the diagram, $$AP=BP$$ So $P$ is the midpoint of the line $AB$. The coordinates of $P$ can be calculated using midpoint formula: $$P(\frac{-2+x}{2},\frac{6+y}{2})$$ Now this point $P$ lies on the line $y=2x$, so: $$\frac{6+y}{2}=2(\frac{-2+x}{2})$$ Solving this you will get, $$2x-y=10$$ Now, since the lines $y=2x$ and $AB$ are perpendicular, the slope of both the lines will follow:

$$m_1m_2=-1$$ Slope of line $y=2x$ is $2$ and that of line $AB$ is : $$m_2=-\frac{1}{2}$$ Now the slope of the line $AB$ is : $$m_2=\frac{y-6}{x+2}=-\frac{1}{2}$$

Solving this you will get: $$x+2y=10$$ Solving the equations: $$2x-y=10$$ $$x+2y=10$$ You will get the values $x=6$,$y=2$. So the reflection of the point is $B(6,2)$.