3

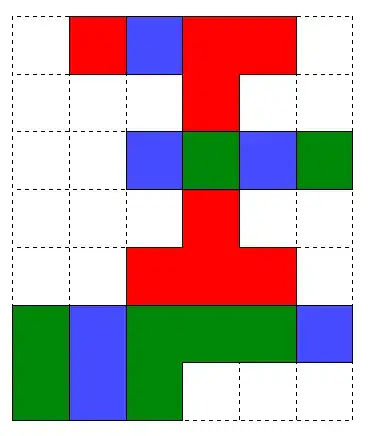
I am trying to unfold a J2 pentacube into a flat net (also non-edge intersecting) such that the net fits in the smallest possible rectangular area.

enter image description here

So far I have managed to unfold it to a 6 by 7 grid:

enter image description here

Note: To aid visual interpretation the colours in this net indicate which plane the face ends up in.

So my question is: Is there a more compact net for this shape?

(I am unfolding several polycubes and J2 has the largest footprint. The other pentacubes I have unfolded fit in a 5x7 or smaller rectangle.)

I do not want to have the green 2x1 rectangle below but not joined to the red square on the top row as it then looks like it is joined.

An extended optional question: are there special techniques/software for unfolding polycubes/polyhedra into nets?

Community
  • 1
Ian Miller
  • 11,844
  • [+1] No clear idea of a program that would generate all unfoldings. Besides, what is "J2" in "J2 pentacube" ? – Jean Marie May 20 '19 at 13:38
  • Is this reference useful : http://cglab.ca/~vida/pubs/papers/Cubigami.pdf ? – Jean Marie May 20 '19 at 13:50
  • Another one : https://www.researchgate.net/publication/322076258_Folding_Polyominoes_into_PolyCubes – Jean Marie May 20 '19 at 16:39
  • Having had a look at (https://courses.csail.mit.edu/6.849/fall10/lectures/), I understand that many people have done a lot of work on these issues, and produced many results... I am convinced that one has to ingerate some of them before taking with bare hands your issue... – Jean Marie May 20 '19 at 16:52

1 Answers1

1

If you're willing to accept non-polyomino nets, here's one that can fit inside a $6.5 \times (5+\epsilon)$ rectangle for arbitrarily small $\epsilon>0$:

enter image description here

RavenclawPrefect
  • 17,299