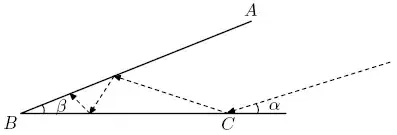
There is a beam of light which strikes $BC$ at the point given in the diagram at an angle $\alpha = 19.94^{\circ}$ with $BC$ and reflects at an equal angle. The reflections continue following the law:
$$\text{angle of incidence} = \text{angle of reflection}$$
The question asks me to find out how many times will the ray get reflected. I analysed its path and came to the inclusion that the direction of light ray will reverse, i.e. it will start coming out of the angle but not following its initial path, after the $36$-th reflection, which occurs at the surface $AB$. But I am unable to analyse further.
Any help would be appreciated. Thanks in advance.