Can numbers with similar stopping times in the Collatz Conjecture be functionally described?

Question

We slightly refine the Collatz sequence as follows:

$$f(n) = \begin{cases} \text{Od}(n) & \text{if } n \equiv 0 \pmod 2\\ 3n + 1 & \text{if } n \equiv 1 \pmod 2\\ \end{cases} $$

Where Od(n) is the odd part of n. And

$$a_i(n) = \begin{cases} n & \text{for } i = 0\\ f(a_{i-1}(n)) & \text{for } i > 0\\ \end{cases} $$

We wish to classify numbers by their refined Collatz stopping times, $C(n) = s$.

$$C(n) = s \iff a_s = 1$$

And we wish to describe sets of natural numbers grouped by stopping time class: $$C_s = \{n\in\mathbb{N} \big| C(n) = s\}$$

Note: \begin{align} C_0 &= \{1\}\\ C_1 &= \{n,a \in \mathbb{N} | n = 2^a\}\\ C_2 &= \bigg\{n,a \in \mathbb{N}, a>1 \bigg|n = \frac{4^a - 1}{3}\bigg\}\\ C_3 &= \{n\in\mathbb{N}, c_1\in C_1, c_2\in C_2\bigg|n=c_1 \times c_2\}\\ C_4 &= \bigg\{n\in \mathbb{N},a_1,a_2 \in \mathbb{Z}^*, r_1\in \{1,2\}, 3a_1+r_1\geq2\bigg|n=\frac{1}{3}\bigg(2^{3 - r_1}\times4^{a_2}\times\frac{4^{3a_1 + r_1} - 1}{3} - 1\bigg)\bigg\}\\ C_5 &= \{n\in\mathbb{N}, c_1\in C_1, c_4\in C_4\bigg|n=c_1 \times c_4\} \end{align}

This seems to be quickly getting out hand. What is $C_6$? What texts might have similar analysis?

Answer 1

I've got myself used to the following notation, which immediately gives a provisorial answer for your question.
I write for one transformation from an odd number $a$ to the next one: $$C(a;A) = {3a+1 \over 2^A}$$ and for more iterations $$C(a;A,B) = {3{3a+1 \over 2^A}+1\over 2^B} $$ and so on, where of course, given some $a$, the $A,B,...$ are completely determined.
But using the inverse of the transformation $$ D(a;A) = {2^Aa-1 \over 3 } \\ D(a;A,B) = {2^B{2^Aa-1 \over 3 }-1 \over 3} \\ $$ and so on leaves freedom for choices of the exponents $A,B,...$, of course with some modular restrictions depending on the choice of $a$.
But provisorially we can state, that the set of numbers with a given number of transformation (or "length of trajectory") is that with a fixed number $N$ of exponents in the $D()$-notation: $$D(1;A_1,A_2,A_3,....,A_N)$$ indicates all numbers of same length of trajectory.

Respecting all the modular conditions on the $A_k$ gives of course not much more simple formula than your approach. For a nice visual approach to see that numbers-of-same-transformation-length $N$ you might like this "bottle-brush"-picture;
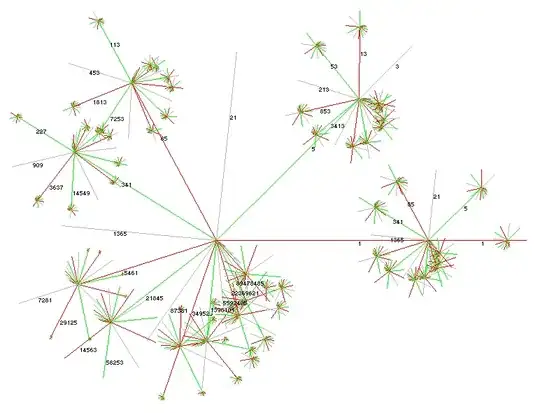
Here, around the center of the "bottle-brush" having the root $1$ are that numbers which have length $N=1$ trajectory - the numbers $1,5,21,85,...$ are written at the whiskers rooting in the center.
Each of this whiskers point now to a new copy of that "root/whisker"-pattern; all numbers written at the whiskers of that copies have trajectory $2$ and so on. Of course all structures here are thought of as being infinite.

I think, there is one valuable simplification of the functional formula possible. To have this, let us talk instead of the odd numbers $a_k$ of their $3a+1$ - images $b_k$. The involved formulae, written on that $b_k$ look much cleaner - and after having such formulae for the transformed $b_k$ we can retransform each $b_k$ to $a_k$ by $a_k = (b_k-1)/3$ .

The well known vector for the odd numbers with transformation length $1$ being $a_k=[1,5,21,85,...]$ transforms to $b_k = [4,16,64,...,4^k,...]$.
The $D()$-notation for the $a_k$ is simply $D(1;A_1)_{A_1=2k}$
From that, the vector of odd numbers with trajectory-lenght $N=2$ meeting the value $a_2=5$ is $a_{2,j}=[3,13,53,...]$ . Again the $b$-notation gives a significant simplification for the human reading: $b_{2,j}=[10,40,160,...,10\cdot 4^{j-1},...]$

I'll leave it so far with that hint at the moment, I think it gives an idea how to proceed on your own. I can come back to this possibly this evening.