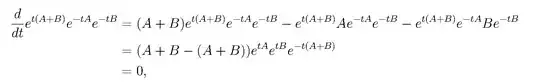 I am trying to understand what happens to the second line of this proof(p8), where the some sketchy combination of exponential terms are performed, which seems to be using the property $$e^{(A+B)t}=e^{At}e^{Bt}$$, we are trying to prove. So this proof seems to be invalid, in my opinion. What am I missing here?
I am trying to understand what happens to the second line of this proof(p8), where the some sketchy combination of exponential terms are performed, which seems to be using the property $$e^{(A+B)t}=e^{At}e^{Bt}$$, we are trying to prove. So this proof seems to be invalid, in my opinion. What am I missing here?
Asked
Active
Viewed 756 times
1
drerD
- 589
-
1this is not true if $A$ and $B4 does not commute. – Tsemo Aristide Jan 28 '18 at 02:57
-
$a^n\cdot a^m=a^{n+m}$. Is that what you're looking for? – Landuros Jan 28 '18 at 02:59
-
1the second line should be $(A+B-(A+B))e^{t(A+B)}e^{-tA}e^{-tB}$ IMO – drerD Jan 28 '18 at 05:19
1 Answers
1
@user14042 has it right in their comment: "there's a mistake in the document you linked, the second line should be $$(A+B-(A+B))e^{t(A+B)}e^{-tA}e^{-tB}."$$
(Honestly, I just assumed that's what it said without bothering to look too deeply at the exponentials. @user14042 has good noticing glasses!)
With that fixed maybe you can see the real work that is being done in line two, which is a few applications of your Lemma 14. For instance, in the second term $e^{t(A+B)}A$ is replaced with $Ae^{t(A+B)}$, which is permitted as $A$ and $t(A+B)$ commute. (It's a bit confusing as your Lemma 14 uses the same variables as your Theorem 15, but with different meanings, so you have to think things like "... so we'll let $B$ be $t(A+B)$...".)
JonathanZ
- 10,615
-
Thanks for confirming my doubt, I got the part where it uses the identify $e^{t(A+B)}A = Ae^{t(A+B)}$, even after this is applied, matrices A, B move to the front of the terms, it should not just become $e^{t(A+B)}e^{−tA}e^{−tB}$, which can be obtained with the exact identify $e^{(A+B)t}=e^{At}e^{Bt}$ I am trying to prove. – drerD Jan 29 '18 at 01:25
-
Oh dear, because you made that observation as a comment and not as part of the original question I didn't notice that "person who made comment" and "person who asked question" were both you -- I'm a little embarrassed. Anyways, yes you are right. And if you know the person who created that PDF you might want to notify them that you're pretty sure you stumbled onto a 'mis-typed expression". It'll save others from having to deal with the same problem, and maybe(?) impress your teacher/TA. – JonathanZ Jan 29 '18 at 01:36
-
thanks for the help, I am not taking this course, just found this pdf randomly while learning about matrix exponentials. – drerD Jan 29 '18 at 04:43