M and n are positive integers such that $2^n - 3^m > 0$. Prove (or disprove) that $2^n - 3^m \geqslant 2^{n-m}-1$.

Question

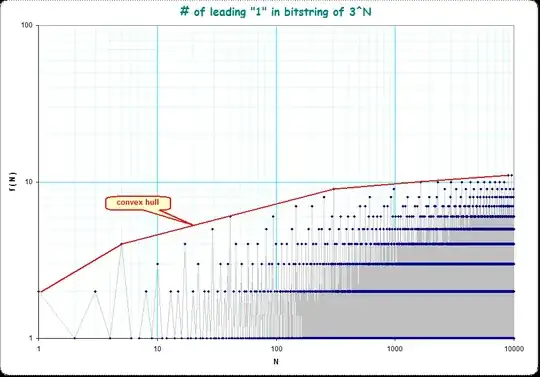
Given that $2^n - 3^m > 0$, I know that $n > m\log_{2}3$ (*). If $2^n - 3^m \geqslant 2^{n-m}-1$, $n>= m + \log_{2}\frac{3^m-1}{2^m-1}$ (**).

This is the result when I graph it out ($m$ -> $x$, $n$ -> $y$): https://i.stack.imgur.com/yRCu7.png (*) and (**) correspond to the red and blue shaded area, respectively. The inequality could be stated that for $m$, $n$ integers, if $(m, n)$ lies in the red area, it's also in the blue area. In other words, there's no in lattice point in the only-red-shaded area.

The mentioned critical region is bounded by the y-axis (given that $m$, $n$ are positive), the straight line $y_1 = x \log_{2}3$, and the curve $y_2 = x + \log_{2}\frac{3^x-1}{2^x-1}$ that approaches $y_1$ as $x$ approaches infinity (proven using limits). Since $\log_{2}3$ is irrational, $y_1$ does not pass through any lattice point (except at origin), and the distance between $y_2$ and $y_1$ gets smaller and smaller as $x$ gets larger, it is more and more unlikely that the critical region passes through some lattice points when $x$ increases. This support my observation that for large m (say $m=100$), $2^n-3^m$ is not just "larger than or equal" to $2^{n-m}-1$ but EXTREMELY larger ($3\cdot 10^{29}$ times larger in this case)! The gap between the two tends to get bigger as m increases, which makes me believe the inequality is true for all numbers.

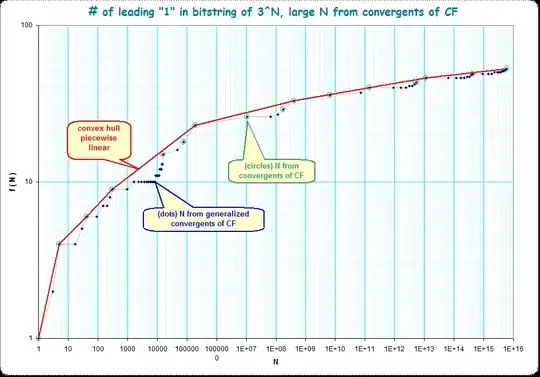
For another approach, I see that the inequality has more chance to fail as $n$ decreases and/or $m$ increases; in other words, we just need to take $n$ as a function $n(m)$ equals to the smallest possible number such that $n > m\log_{2}3$. Since $n$ is integer, $n(m) = \lceil m\log_{2}3\rceil$.

Now replace $n$ with $n(m)$ in (**): $$\lceil m\log_{2}3\rceil \geqslant m + \log_{2}\frac{3^m-1}{2^m-1}.$$ Subtract both sides by $\log_{2}(3)m$: $$\lceil m\log_{2}3\rceil - m\log_{2}3 \geqslant \log_{2}\frac{3^m-1}{2^m-1} - m\log_{2}\left(\frac{3}{2}\right).$$ The left side of the inequality is the difference of $m\log_{2}3$ and its rounded-up integer, the right side is the difference of $y_2$ and $y_1$ in the graphing section. Here is the graph of the two: https://i.stack.imgur.com/sxwjY.png Blue and red line correspond to left and right side, respectively; horizontal axis represents $m$. As seen, the left side values jumps back and forth somewhere between $0$ and $1$, while the right approaches zero very quickly (already $0.000175$ at $m=13$), so I hypothesized that the inequality is always true, which would prove the conjecture in my question. However, I have no idea where to go next, since the value of $\lceil m\log_{2}3\rceil - m\log_{2}3$ looks pretty "random" to me; I mean, $m\log_{2}(3)$ is an irrational number (has infinitely many decimal values with no pattern), how can I predict the difference of its rounded-up integer and itself?

By the way, I noticed this inequality while trying to solve the Collatz conjecture, and I'm just curious whether it's really true for all numbers or not (I have checked it with computer for m up to 10 billion). My approach above might be completely wrong, so don't just stick with it. I appreciate any thoughts/suggestions of yours about this conjecture or directions I should go that may help proving this.

Thanks a lot.

Answer 1

Answer: Possible counter-examples must satisfy $m<e^{28}$ and $n<e^{29}$, hence only a finite number of them may exists. This follows by Baker's theorem about lower bounds of linear forms of logarithms.

---

For prove it, let $(m,n)$ be a counter example, that's $3^m <2^n <3^m+2^{n-m}-1$. We get $$\begin {align} 0 <n\log (2)-m\log (3) &<\log\frac {1-3^{-m}}{1-2^{-m}}\\ &<\frac {1-3^{-m}}{1-2^{-m}}-1\\ &<2^{-m} \end {align}$$

By Baker's theorem there exists an effective constant $C$ (not depending on $n,m$) such that $$n\log (2)-m\log(3) >n^{-C} $$ for all $n,m$ such that $n\log (2)-m\log(3) >0$.

This leads to $n^{-C}<2^{-m } $ which implies $\frac m{\log(n)}<\frac C{\log(2)}$ hence $\frac m {\log (n)} $ is bounded by an effective constant. On the other hand $n\log (2)-m\log (3)<2^{-m}<1$ gives $\log (n)<\log (m)+1$ hence \begin{align*} \frac m {\log (m)} &\leq\frac{3m}{1+\log(m)}\\ &<\frac{3m}{\log(n)}\\ &<\frac{3C}{\log(2)} \end{align*}

that's $\frac m {\log (m)} $ is bounded as well by an effective constant.

By effectivness of the constant, is enough to verify the impossibility of $3^m <2^n <3^m+2^{n-m}-1$ for finitely many values of $m,n $.

In particular, the explicit result by Baker and Wüstholz states: \begin{align*} &\log|\Lambda|>-C'h(\alpha_1)h(\alpha_2)\log(\max\{|\beta_1|,|\beta_2|\})\\ &C'=18(n+1)!n^{n+1}(32d)^{n+2}\log(2nd) \end{align*} where $\Lambda=\beta_1\lambda_1+\beta_2\lambda_2$ and in our case \begin{align*} &\beta_1=n& &\lambda_1=\log(\alpha_1)& &\alpha_1=2\\ &\beta_2=-m& &\lambda_2=\log(\alpha_2)& &\alpha_2=3 \end{align*} hence $h(\alpha_i)=\alpha_i$, $d=1$ and $n=2$. Since $C=C'h(\alpha_1)h(\alpha_2)$, with these values, we get: $$C=18\cdot 3!\cdot 2^3\cdot 32^4\cdot\log(4)\cdot 2\cdot 3<8\cdot 10^9$$ from which $$\frac m{\log(m)}<4\cdot 10^{10}$$ which is satisfied for $m<e^{28}$. Thus, possible counter-examples are bounded by $m<e^{28}$. Since $\log(n)<\log(m)+1$ we have $n<e^{29}$, hence only a finite number of counter-examples may exists.

Answer 2

Answer: There are at most finitely many counterexamples. This is related to the irrationality measure $\mu$ of $\log 3/\log 2$, which is finite (and effectively boundable) according to this article by Yann Bugeaud, Theorem 1.1. What I don't know is whether we can bound the possible counterexamples.

---

We have by the mean value theorem for $\exp$: $$\begin{align*}2^n-3^m &\geq 3^m (n\log 2-m\log 3)\\ &\geq 3^m n\log 2 \cdot n^{-\mu-\varepsilon}\end{align*}$$ for (say) $\varepsilon=0.1$, except for possibly a finite number of pairs $(m,n)$ coming from exceptionally good approximations of $\log3/\log 2$.

To finish, the idea is that either the inequality is trivial, or $3^m$ is sufficiently close to $2^n$ to show that this is larger than $2^{n-m}$.

Note that (less important)

• $m\leq n-1$ except for small values
• We may ignore the $+1$ in the RHS because the LHS is odd

and more importantly:

• If $2^{n-1} \geq 3^m$ it is trivial, becaue $2^n-3^m > 2^{n-1} \geq 2^{n-m}$

so that we may assume $3^m\geq 2^{n-1}$.

Now $$6^m \geq 6^{(n-1)\log2/\log 3} > 3^{n-1}$$ (use a calculator for the last inequality) so that $$3^m >2^n/2^m \cdot 1.5^n \cdot\tfrac13=2^{n-m}\cdot 1.5^n\cdot\tfrac13$$ where we keep the $1.5^n$ to take care of factors $n^{-\ldots}$.

Combining everything, $$\begin{align*} 2^n-3^m &\geq 3^mn\log 2 \cdot n^{-\mu-\varepsilon}\\ &>2^{n-m}1.5^n\cdot\tfrac13\cdot n\log 2 \cdot n^{-\mu-\varepsilon}\\ &>2^{n-m}\end{align*}$$ for $n$ sufficiently large (because $\mu$ is finite!), except for possibly a finite number of pairs $(m,n)$.

Answer 3

I add this comment (not an answer) because you wrote that you tested your conjecture heuristically up to large $m$. I think I provide an interesting further insight.

---

If you ask for $$2^n-3^m \ge 2^{n-m}-1 $$ we can look at it in another interesting way. But let us first introduce the shorter notation $b=n-m$ . Now let us describe $2^n$ and $3^m$ in terms of $2^b$ where $M$ and the residue $r$ with $0 \lt r \lt 2^b$is formally introduced: $$2^b \cdot 2^m-(M \cdot 2^b + r) \ge 2^b-1 \\ 2^b \cdot (2^m-M) -r \ge 2^b-1 \\ 2^b \cdot (2^m-M) \ge 2^b+r-1 \\ 2^m-M \ge 1 + {r-1 \over 2^b} \\ $$ Here the rhs is in the interval $1 \le (\text{rhs}) \lt 2$ We see, that only for any $M=2^m-1$ this is false if not also $r=1$. Thus the inequality holds, if $M$ is indeed smaller than $2^m-1$. In bitstring-notation this means, if there is a zero in the bitstring of $M$. This is of course the case in all empirical observations, except for $m=1$ where $b=1$ and $3^1 = M \cdot 2^b + r = (2^1-1)\cdot 2^1 + 1$ .

The idea of simply looking at the position of the first zero in $M$ is very intriguing and strongly gives evidence for the truth of your inequality. Even the following graph suggests hope that perhaps a functional upper bound of the length of the leading "1"-bitstring might be found. I've made three images of different resolution. Note, that for my own convenience I used $N$ for what you call $m$ and $S$ for what you call $n$ and $B=S-N$ for what is $n-m$ in your formula.

And zooming out up to $N=10000$ it suggests there might by a functional bounding for the position of the first occuring zero/for the length of the leading bitstring of "1" (see the read convex hullcurve)

The hullcurve, btw., matches the positions $N$ which occur in the convergents of the continued fraction of $\log_2(3)$ .
A larger view, only plotting convergents and generalized convergents again suggests a hullcurve which might be convex on the long run: