I was wondering what the least dense rigid uniform packing of congruent spheres was. The lowest density packing of circles is the truncated hexagonal packing.
-
3There are rigid circle packings with arbitrarily low density: see http://mathworld.wolfram.com/RigidCirclePacking.html. – mjqxxxx Nov 24 '12 at 18:49
-
Both the Wikipedia and the Mathworld articles on sphere packing cite a book by Martin Gardner as the reference for the loosest rigid sphere packing. Unfortunately, the articles don't tell us anything about this packing except that is has a density of 0.0555. – begeistzwerst Nov 24 '12 at 19:15
-
@mjqxxxx: Why does the link imply that one can have arbitrarily low density? I do not think the pictured construction can be iterated, as the adjacent circles are no longer at $120^\circ$ angles. – RavenclawPrefect Feb 24 '21 at 02:30
3 Answers
It appears these very loose packings are not lattice packings. They are periodic, but given a fixed origin, if there are spheres centered at vectors $u,v$ there may not be a sphere centered at $u+v.$ Instead, a condition referred to as rigid or jammed is used.
Gardner, page 88:
=-=-=-=-=-=-=-=-=
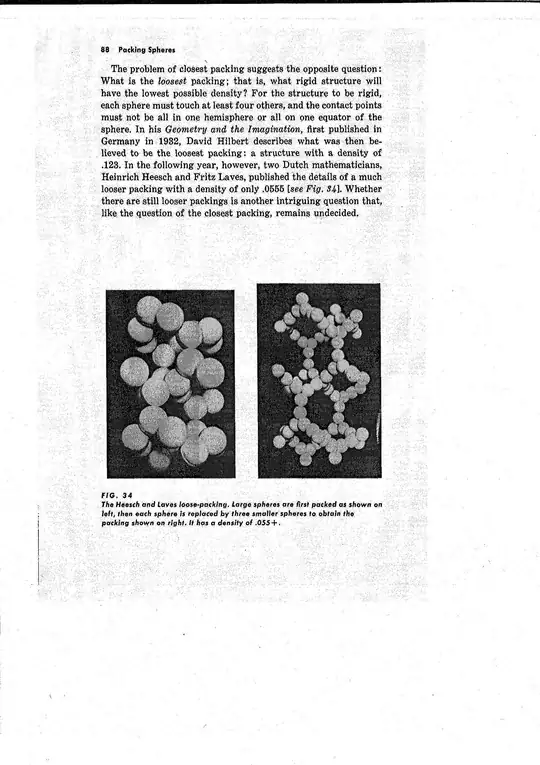
=-=-=-=-=-=-=-=-=
Hilbert and Cohn-Vossen, pages 50-51:
=-=-=-=-=-=-=-=-=

=-=-=-=-=-=-=-=-=
- 139,541
The answer seems to depend on what the restrictions are; Fischer and Dorozinski & Fischer present sphere packings of arbitrary low density. See also Dorozinski's web page (in German; English translation by Google here).
- 5,862
There are many. They all have arbitrarily low density. Same with circles. Here you can find some: https://arxiv.org/pdf/0908.1830.pdf
Also note that even in case you restrict your question to uniform-coordination systems, the lowest density packing of circles is not the truncated hexagonal packing. Flakene is less dense: https://arxiv.org/pdf/1811.01112.pdf
- 91