0

Why does the Newton-Raphson method for solving equations always work?

What I know:

  • I know that if $f(x) = 0$, then the Newton-Raphson method may be applied. It states that $$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$$ where the solution to $f(x) = 0$ is $x_\infty$

  • I also know that you can select a point on the graph of $f(x)$ (your first estimate $x_1$), and Newton-Raphson takes the gradient of that point, and where that gradient meets the $x$-axis, and the x value is where $x_2$ is.

Newton Raphson

I know how it works, but why the $$\frac{f(x)}{f'(x)} ?$$

It seems that the curve is divided by the gradient, but what does this give?

I would just like an explanation of why this works.

Xetrov
  • 2,089
  • See this question. – C. Falcon Jun 01 '17 at 12:56
  • It does not always work. – Travis Willse Jun 01 '17 at 13:01
  • Consider $f(x) = x^3 - x$. It has a zero at $x = 0$. If you start your N-R iteration at $$ x_0 = a = \sqrt{\frac{1}{5}} $$ you'll find that $x_1 = -a$, $x_2 = a$, $x_3 = -a$, and so on. These values bracket the root at $x = 0$, but do not converge to it. – John Hughes Jun 01 '17 at 13:17
  • The question (at least the one in the header and the very first sentence) is NOT answered by the thing the link points to. (In particular, the failure of the method to work when you start from the wrong initial guess isn't really discussed there.) – John Hughes Jun 01 '17 at 13:19

1 Answers1

2

What I can give you is a derivation of the method.

Assume some $x^*$ is some zero of $f$. Bcause $f$ is differentiable, sufficiently close at $x^*$ it looks like a straight line. So when you are not exactly in $x^*$ but close to it, then you can just take this line and look where this line intersects the $x$-axis instead of the more complicated function $f$. This is because the zeros of a linear function are very easy to determine. E.g. for $y=mx+n$ the zero is simply at

$$x =-\frac nm.$$

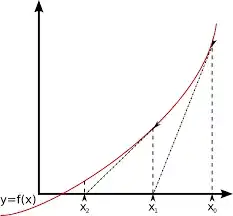
So say we are in $x_i$, close to $x^* $. At this point the curve looks like the line

$$y=f'(x_i)(x-x_i)+f(x_i).$$

This is the unique linear function through $f(x_i)$ with the appropriate slope to be a tangent to $f$. Now what is the unqiue zero $x$ of this line? Set $y$ to zero and rearragne and you will find

$$x=x_i-\frac{f(x_i)}{f'(x_i)}$$

in analogy to the zero for a general linear function $y=mx+n$. So when we call this new zero $x_{i+1}$, then starting from an estimation of a zero $x_i$, we found a better one.

This is essentially what the method does. It take an approximation and makes a better one. When your approximation is bad, so will the result be bad too (maybe).

Note:

Newtons method does not always work. There are examples where the sequence of $x_i$ either diverges or oscilltes, either because there is no zero or your initial estimation was bad.

M. Winter
  • 29,928