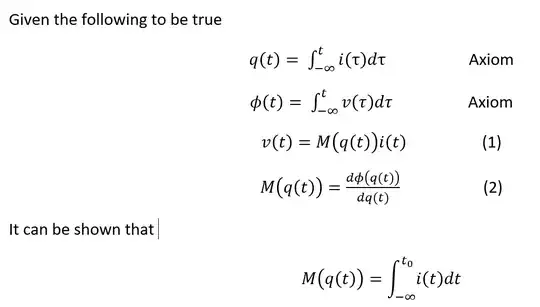1

I know this is not the EE stack exchange. I have tried there, no one is replying. Since this revolves around math, and Chua is laying down the mathematical framework for the memristor, I don't believe posting here is too inappropriate.

I'm going through Chua's 1971 memristor paper. I am stuck on a part that I believe in pretty crucial. It is

Observe that the, value of the incremental memristance (memductance) at any time to depends upon the time integral of the memristor current (voltage) from t = - co to t= to. Hence, while the memristor behaves like an ordinary resistor at a given instant of time to, its resistance (conductance) depends on the complete past history of the memristor current (voltage). - Page 511(page 5 of the pdf) top of the right column

http://www.cpmt.org/scv/meetings/chua.pdf

I'm not seeing the integral from any of the equations 1 through 4 that are presented in the paper.

When I read the section in question, this is what comes to mind, but I cannot see the derivation. Am I thinking about this incorrectly?

enter image description here

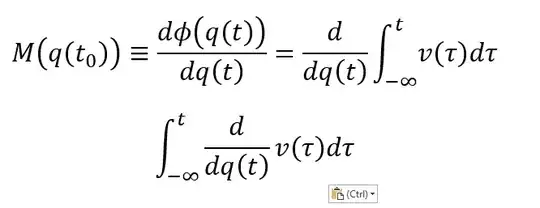
To expand further on what I have tried enter image description here

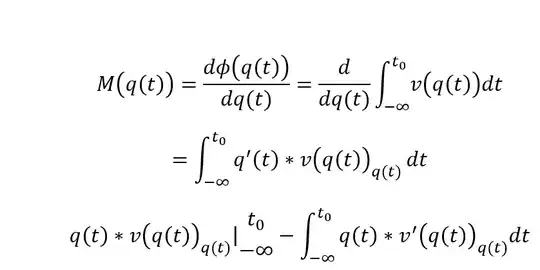
and have thought of phi(t) as a composite function ( by equation 2) enter image description here

The q(t) subscript denotes the with respect to q(t), prime is with respect to t.

at this point, if you apply a 2nd iteration of integration by parts, you can go two ways, let the anti derivative be q'(t), in which case you are back to square 1 or you can apply n iterations to v'(t)_q(t)

Does anyone see anything glaringly wrong with my math? Is it a physics thing possibly? I'm not seeing how current gets into this at all. I realize memristors is a rather newish topic that not many people are aware of or even care about.

Melendowski
  • 139

1 Answers1

0

I think that you have misunderstood the proposition of Chua: "Observe that the value of the incremental memristance (memductance) at any time $t_0$ depends upon the time integral of the memristor current (voltage) from $t = - \infty $ to $t= t_0$."

In fact the observation just says that $M $ is function of the integral of the current $$ M=M (q(t_0))=M\left ( \int_{-\infty}^{t_0}i (\tau)\mathrm d \tau\right) $$ and that $W $ is function of the integral of the voltage $$ W=W (\varphi(t_0))=W\left ( \int_{-\infty}^{t_0} v(\tau)\mathrm d \tau\right) $$

You have nothing to calculate.

alexjo
  • 14,976