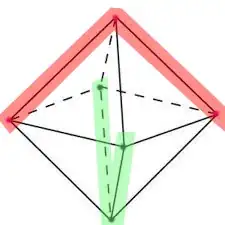
Consider a regular solid octahedron, which includes the interior. Let $r$ be the subset consisting of the top vertex, two vertices adjacent to it but not to each other, and the two edges between them, as in the diagram above. Let $g$ be the congruent subset constructed on the two edges and three vertices that do not intersect $r$.
Now color every point of the octahedron red if it is closer to some point of $r$ than to any point of $g$, and conversely green if it is closer to $g$ than to $r$. We can call the sets of red and green points $R$ and $G$; by symmetry, they are congruent. The boundary between them is the (two-dimensional) set $B$ of all points equidistant from $r$ and $g$.
What does $R$ look like? What shape is the boundary $B$?
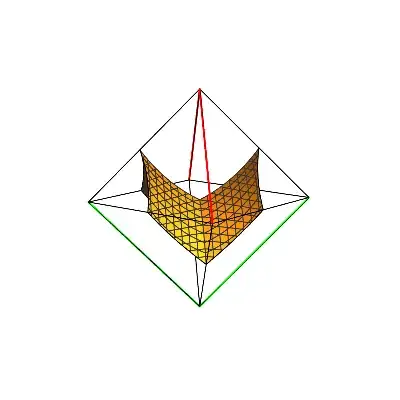
It appears to me that the intersection of $B$ and the surface of the octahedron is a wiggly, approximately cubical loop made from eight parabolic segments joined end to end to end, but I am not certain.
It also seems plausible that $B$ is obtained from this wiggly loop by taking the union of the straight segments from the points of the loop to the center $O$ of the octahedron, but again I am not sure.
In any case I am not able to visualize what this actually looks like or what the congruent solids $R$ and $G$ look like.