Compute $$\int\limits_{0}^{\infty}\frac{1}{(x+e)(\ln^{2}x + 4\pi^{2})} \, dx$$
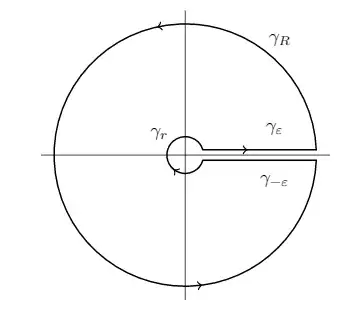
Using the substitution $u = \sqrt{x}$ we see that \begin{align*} \int\limits_{0}^{\infty}\frac{1}{(x+e)(\ln^{2}x + 4\pi^{2})} \, dx =\frac{1}{2} \int_{0}^{\infty} \frac{u}{(u^{2}+e)(\ln^{2}u + \pi^{2})} \, du \end{align*} Now let $f(z) = \frac{z}{(z^{2}+e)\ln z}$ with branch cut along the positive real axis and $-\pi \leq \arg z < \pi$. Let $\gamma$ be the following contour:
Going by residues, we have that $$\oint_{\gamma} f(z) \, dz = 2\pi i \left(\frac{2}{1+\pi^{2}} + \frac{1}{1+e}\right)$$ The same tricks as always show that the contributions from $\gamma_{R}$ and $\gamma_{r}$ will vanish as $R$ goes to infinity and $r$ goes to 0. Now \begin{align*} &\oint_{\gamma} f(z) \, dz = \oint_{\gamma_{\varepsilon}} f(z) \, dz + \oint_{\gamma_{-\varepsilon}} f(z) \, dz \\ =& \int_{0}^{\infty} \frac{u+i\varepsilon}{((u+i\varepsilon)^{2}+e)(\ln (u+i\varepsilon)}\, du - \int_{0}^{\infty} \frac{u-i\varepsilon}{((u-i\varepsilon)^{2}+e)(\ln (u-i\varepsilon))}\, du \end{align*} Taking $\varepsilon$ to $0$ $$= 2\pi i \int_{0}^{\infty}\frac{u}{(u^{2}+e)(\ln^{2} u + \pi^{2})} \, du $$ Putting it all together, we finally see that $$\int\limits_{0}^{\infty}\frac{1}{(x+e)(\ln^{2}x + 4\pi^{2})} \, dx = \frac{1}{2}\left(\frac{2}{1+\pi^{2}} + \frac{1}{1+e}\right) $$ The professor said everything is good except that I put $\arg z \in [-\pi, \pi)$. I'm taking the positive real axis to the angle $-\pi$ and going all the way around comes to $\pi$. This issue is fixed by taking $0 \leq \arg z < 2\pi$ and changing $\ln z$ to $(\ln z - \pi i)$ in the denominator. This example does something weird and I think similar to what I did. Can someone explain why what I did wasn't okay? I don't really understand.