1

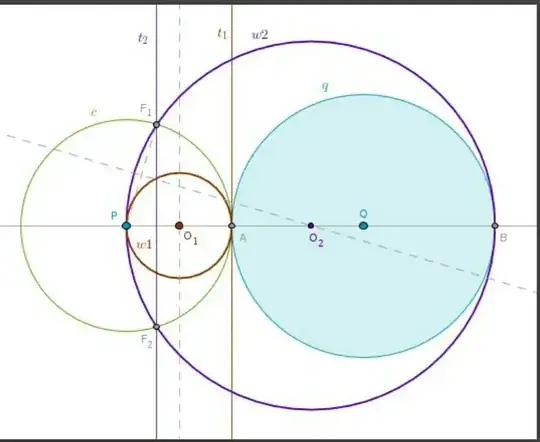
enter image description here Consider the inversion of circles ($w_1$ and $w_2$) w.r.t. the circle ($c$) that gives circles of infinite radius ($t_1$ and $t_2$ respectively). What is the nature of the generalised circles $t_1$ and $t_2$ (are they intersecting at one point OR concentric)? Is it possible to get $t_1$ and $t_2$ such that they are concentric circles of infinite radius?

user376343
  • 8,311
user402705
  • 35
  • Can we say that the parallel lines t1 and t2 meet at a point at infinity ? – user402705 Jan 22 '17 at 14:08
  • Yes inversion moves the center of the inversion circle to infinity – Willemien May 26 '17 at 17:40
  • Thank you for the reply. Is there a concept such as concentric circles of infinite radius( if we imagine the circle t1 to be moved half the distance between t1 and t2 ,then we ge t two concentric circles of infinite radius). – user402705 May 26 '17 at 18:00
  • Not sure but there is something like the angle between the circles w1 and w2 in your example they are tangent to each other so the lines are parallel – Willemien May 26 '17 at 18:18

0 Answers0