0

Is it possible to obtain two concentric generalised circles(parallel straight lines) through inversion of two circles w.r.t a third circle?

user402705
  • 35
  • If the center of the inversion does not belong to any of the given lines, the image of such lines will be circles through the inversion center, i.e. two intersecting circles. On the other hand, if the inversion center lies on one of the two initial lines, the image of a line is still a line. So no. – Jack D'Aurizio Jan 21 '17 at 14:03
  • However, given two circles one inside the other, you may find an inversion that maps them into two concentric circles: http://mathworld.wolfram.com/LimitingPoint.html – Jack D'Aurizio Jan 21 '17 at 14:05
  • Does the inversion of two circles (one within the other) which are passing through the center of inversion (of a larger inverting circle) give rise to two concentric circles ? – user402705 Jan 21 '17 at 14:17
  • How can two disjoint circles pass through the same point?! – Jack D'Aurizio Jan 21 '17 at 14:18

2 Answers2

2

ParallelInvrsns

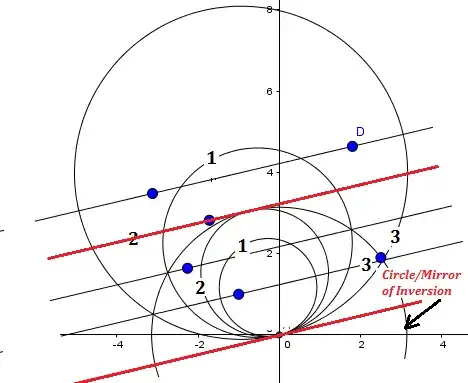
Some parallel line segments are shown reflected about a unit circle centered at origin as mirror ( feature available in Geogebra). When parallel lines go to $ \infty,$ then their images inside the inversion circle tend to go to the origin, being tangent only at an infinite distance from the farthest points .. a feature of hyperbolic geometry. The images can never be concentric just as in both the Poincare's models ( semi-infinite plane or disk.)

EDIT 1:

nvesnParllLines

Inversions of a set of parallel lines bear same label in the figure above.

A set of parallel lines have co-tangential circular inversions.

These inversions have either to be co-tangential or con-centric but not both at the same time !!

Narasimham
  • 40,495
  • If we consider the inversion of circles to get parallel lines(generalised circles of infinite radius),is it possible to obtain parallel lines( generalised circles) that are concentric? – user402705 Jan 22 '17 at 04:58
  • In the answer the inversion of lines was considered,please consider the inversion of circles that gives concentric circles of infinite radius. Thanks for the answer. – user402705 Jan 22 '17 at 05:07
  • I am unable to understand the comment immediately above.In a partial answer to the one above it I can only say:::: Basically inversions are a homothety or scaling in a similitude situation, I shall reply in EDIT1 soon,... to the extent that I can understand.. . – Narasimham Jan 22 '17 at 16:02
  • If we consider the parallel lines in EDIT 1 as generalised circles of infinite radius, then is it possible for them to be concentric? Or do these generalised circles(straight lines) meet at infinity ,similar to the original circles that meet at the center of inversion ? (Thanks for the answer) – user402705 Jan 22 '17 at 16:32
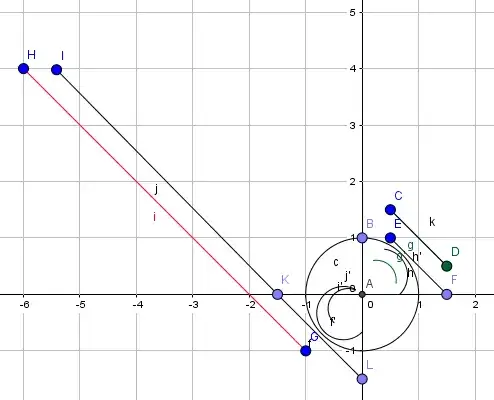
  • Please see the question titled :parallel lines as generalised circles in inversive geometry? It is the same question as above but I included a figure to make the question more clear? – user402705 Jan 22 '17 at 17:22
0

can the two straight lines in the figure be concentric circles in any case ? Or if we have two parallel lines is it possible that they are concentric generalised circles?

enter image description here

user402705
  • 35
  • If we consider two generalised circles (parallel lines) ,which are obtained through the inversion of two circles touching each other only at the center of inversion,then is it possible for the lines to be concentric circles ? Does the larger circles(lines) also touch each other at one point (like the smaller circles before inversion)? – user402705 Jan 21 '17 at 14:47