The equation for the first line is $y = \frac{1}{2}x - 2$, and the equation for the second line is $y = 2x + 1$. They intersect at $(-2, -3)$.
Someone told me I can just average the slopes of the two lines to find the slope of the bisector, but I'm not sure if it's right.
If you have two lines
$$ L_1 : a_1x+b_1y+c_2 = 0 $$
and
$$ L_2 : a_2x + b_2y + c_2 = 0, $$
then the equation of their bisectors is given by
$$ \frac{a_1x+b_1y+c_1}{\sqrt{a_1^2+b_1^2}} = \pm \frac{a_2x+b_2y+c_2}{\sqrt{a_2^2+b_2^2}}. $$
where the $+$ and $-$ make the difference between the two bisectors. You just simplify each equation and read off the slope.
The suggestion you got is completely wrong. In this particular case, you can just notice that lines whose slopes are reciprocals, are symmetric with respect to lines with slope $+1$ and $-1$.
To be on right track, let $Ax + By + C =0, ax + by + c =0 $ be the equations of the given straight lines.The angular bisector is a straight line locus so that length of perpendiculars dropped from it onto the given lines are equal. The polar form of straight line is useful here.
$$ \frac{Ax+By+C}{\sqrt{A^2+B^2}} = \pm \frac{ax+by+c}{\sqrt{a^2+b^2}}. $$
The $+$ sign is taken when the arms contain the origin for internal bisector, $-$ sign for the external bisector perpendicular to it. You can now find its slope.
Take the unitary vectors parallel to the lines: their sum will be parallel to one of the bisecting line, their difference will be parallel to the other one.
To determine which is the one bisecting the acute /obtuse angle, just take the dot product of the two vectors:
note: this method is valid also in 3D. In 2D you can apply the same method to the normal (instead than parallel) unitary vectors.
in your example (using parallel vectors)
Rewrite the line equations in the proportional form $$ \left\{ \begin{gathered} y = \frac{1} {2}x - 2\quad \Rightarrow \quad \frac{{x - 0}} {2} = \frac{{y - \left( { - 2} \right)}} {1} \hfill \\ y = 2x + 1\quad \Rightarrow \quad \frac{{x - 0}} {{1/2}} = \frac{{y - 1}} {1}\quad \Rightarrow \quad \frac{{x - 0}} {1} = \frac{{y - 1}} {2} \hfill \\ \end{gathered} \right. $$
then the parallel unitary vectors are $$ \mathbf{u} = \frac{1} {{\sqrt 5 }}\left( {2,1} \right)\quad \mathbf{v} = \frac{1} {{\sqrt 5 }}\left( {1,2} \right)\quad 0 < \mathbf{u} \cdot \mathbf{v} = \frac{4} {5} $$ and the angle between them is acute. Their sum and difference is $$ \mathbf{u} + \mathbf{v} = \frac{1} {{\sqrt 5 }}\left( {3,3} \right)\quad \mathbf{u} - \mathbf{v} = \frac{1} {{\sqrt 5 }}\left( {1, - 1} \right) $$ and the equations of the bisecting lines will be: $$ \left\{ \begin{gathered} \frac{{x - x_{\,c} }} {3} = \frac{{y - y_{\,c} }} {3}\quad \Rightarrow \quad x + 2 = y + 3\quad \Rightarrow \quad y = x - 1\;\;acute \hfill \\ \frac{{x - x_{\,c} }} {1} = \frac{{y - y_{\,c} }} {{ - 1}}\quad \Rightarrow \quad x + 2 = - y - 3\quad \quad \Rightarrow \quad y = - x - 5\;\;obtuse \hfill \\ \end{gathered} \right. $$
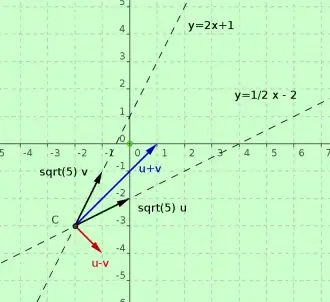
Line 1 is $y = \frac 12 x - 2$. Line 2 is $y = 2x +1$. They intersect at $(-2-3)$.
If on line 1 you go over on $x$ $2$ units you will go up on $y$ by $1$ unit. This will put you at $(0, -2)$. The distance traveled is $\sqrt {1^2 + 2^2} = \sqrt{5}$.
If on line 2 you go over on $x$ $1$ units you will go up on $y$ by $2$ unit. This will put you at $(-1, -1)$. The distance traveled is $\sqrt {2^2 + 1^2} = \sqrt{5}$.
The angle bisector will go through the midpoint of $(0,-2)$ and $(-1,-1)$$*$. So the angle bisector will go through $(-\frac 12, -1\frac 12)$. So the angle bisector goes through the point $(-2,-3)$ and $(-\frac 12, -1\frac 12)$ so the slope is $\frac{-1\frac 12 - (-3)}{-1\frac 12 -(-2)} = \frac {1\frac 12}{1\frac 12} = 1$.
$*$ because... $A = (-2,-3); B= (0,-2); C=(-1,-1);$ and $AB$ = $AC= \sqrt{5}$ so $\triangle BAC$ is isoceles, and the angle bisector of $\angle BAC$ passes through the midpoint of $BC$.
==== details in general ====
You friend is not quite right. You can average the angles but slopes are not angles and there is not a linear conversion between them. (There is a trigonometric conversion between them. But not a linear conversion.)
Bear with me.
Suppose the two lines intersect at $(u,v)$ and line $1$ has slope $m$ and line $2$ has slope $n$.
Move along the line $1$ from $(u,v)$ a distance of $1$ unit. You will have move $\delta $ in the $x$ direction and $m*\delta $ in the $y$ direction so your total distance is $\sqrt{\delta^2 + m^2\delta^2} = 1$.
So $\delta\sqrt{1 + m^2} = 1$ so $\delta = \frac 1{\sqrt{1 + m^2}}$.
So the point on line $1$ that is one unit away form $(u, v)$ is the point $(x_1, y_1) = (u + \frac 1{\sqrt{1 + m^2}}, v + \frac m{\sqrt{1 + m^2}})$.
Likewise the point on line $2$ that is one unit away from $(u,v)$ will be the point $(x_2, y_2) = (u + \frac 1{\sqrt{1 + n^2}}, v + \frac n{\sqrt{1 + n^2}})$
The angle bisector will contain the midpoint of $(x_1, x_2)$ and $(x_2, y_2)$.
The midpoint is $(x_m, y_m) = (u + \frac{[\frac 1{\sqrt{1 + m^2}}]+[\frac 1{\sqrt{1 + n^2}}]}2, w + \frac{[\frac m{\sqrt{1 + m^2}}]+[\frac n{\sqrt{1 + n^2}}]}2)$.
So.... the slope of the angle bisector will be:
$\frac {y_m - v}{x_m - u}= \frac{\frac{[\frac m{\sqrt{1 + m^2}}]+[\frac n{\sqrt{1 + n^2}}]}2}{\frac{[\frac 1{\sqrt{1 + m^2}}]+[\frac 1{\sqrt{1 + n^2}}]}2}=$
$\frac{[\frac m{\sqrt{1 + m^2}}]+[\frac n{\sqrt{1 + n^2}}]}{[\frac 1{\sqrt{1 + m^2}}]+[\frac 1{\sqrt{1 + n^2}}]}=\frac{m\sqrt{1 + n^2}+n\sqrt{1 + m^2}}{\sqrt{1 + m^2}+\sqrt{1 + n^2}}$
$[\frac{m\sqrt{1 + n^2}+n\sqrt{1 + m^2}}{\sqrt{1 + m^2}+\sqrt{1 + n^2}}=\frac{\frac 12\sqrt{1 + 2^2}+2\sqrt{1 + \frac 12^2}}{\sqrt{1 + \frac 12^2}+\sqrt{1 + 2^2}}=\frac{\sqrt{5}/2+ \sqrt{5}}{\sqrt{5}+ \sqrt{5}/2}=1]$
Which... I must confess is a formula I never learned and would never expect anyone to memorize. I'd expect if one needs to find the slope of an angle bisector one would calculate it for the specific lines.
You might be able to simplify that equation further.
=====
That equation is sort of an "average"; just not a standard arithmetic average.
You can calculate the average of the angles of the lines. But slopes are not angles and do not have a linear conversion.
If you know trigonemetry:
Slope = $\frac{rise}{run} = \frac{\sin \theta}{\cos \theta} = \tan \theta$ so the angle of a line is $\theta = \arctan m$.
So the angle of the angle bisector is $\psi = \frac {\theta + \omega}2 = \frac {\arctan(m) + \arctan(n)}2$
And the slope of the angle bisector is $k = \tan(\psi) = \tan(\frac {\arctan(m) + \arctan(n)}2)=\frac{m\sqrt{1 + n^2}+n\sqrt{1 + m^2}}{\sqrt{1 + m^2}+\sqrt{1 + n^2}}$
The vector solution is beautiful, but the typical way would be using the fact that $m=\tan(a)$ where $a$ is the angle respect to the horizontal then the angle of th bisector will be $(\arctan (.5) +\arctan(2))/2$ in this case $45$ so m of bisector is $1$ and the bisector line $y=x-1$
