4

I read from the MGB stats textbook which says something about "the problem of moments", as follows: "In general, a sequence of moments μ1,μ2..,μn,... does not determine a unique distribution function；..., However, if the moment generating function of a random variable did exist, then this moment generating function did uniquely determine the corresponding distribution function "

It is hard for me to see the difference between these two concepts（sequence of moments VS moment generating function). I've looked through several posts about this topic, and I know that someone did come up with a counterexample of a particular density family with the same sequence of moments:

enter image description here

I also read about the proof of the uniqueness of moment generating function.

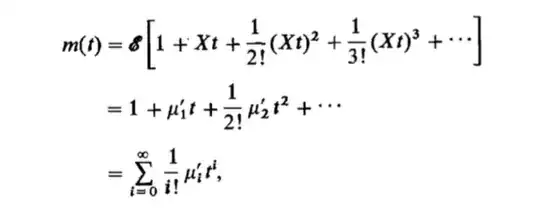
But doesn't that sequence of moments define a moment generating function? As m(t) can be written as enter image description here

Can someone fill the gap for me? Thanks so much!

Zoe Lee
  • 155

1 Answers1

4

The problem is that the series for the moment generating function $m(t)$ might not converge anywhere except $t=0$. The actual result is that if this series has positive radius of convergence, it uniquely determines the distribution.

In your example, the moments are $\mu_n = (4n+3)!/6$, and it's easy to see using the Ratio Test that the radius of convergence is $0$.

Robert Israel
  • 448,999
  • So you are saying "series of moments having positive radius of convergence" equals to "moment generating function exists". And when you say converge, you mean μn converges as n goes to infinity? – Zoe Lee Oct 23 '16 at 17:39
  • Yes: it's not much of an existence if the moment generating function is defined only at $0$.
  • No, I mean the series $m(t) = \sum_{n=0}^\infty \frac{\mu_n}{n!} t^n$ converges.
    • – Robert Israel Oct 23 '16 at 19:15