Suppose that the disk has radius $R$ and rotates with angular velocity $\omega$. In the lab frame $(x,y)$, the trajectory of the red ball can be written parametrically as
$$x(t)=R\left(-1+\frac{\omega t}{\pi}\right) \tag 1$$
where $t\in \left[0,\frac{2\pi}{\omega}\right]$.
In the moving frame $(x',y')$, the trajectory of the "red ball" can be described parametrically by
$$\begin{align}x'(t)&=\cos(\omega t)x(t) \tag 2\\\\
y'(t)&=-\sin(\omega t)x(t) \tag 3\end{align}$$
Transforming the moving frame as expressed in $(2)$ and $(3)$ to polar coordinates $(\rho',\phi')$ and using $(1)$, we find
$$\begin{align}
\rho'^2&=x'^2+y'^2\\\\
&=R^2\left(1-\frac{\omega t}{\pi}\right)^2 \tag 4\\\\
\tan(\phi')&=\left(\frac{y'}{x'}\right) \\\\
&=-\tan(\omega t) \tag 5
\end{align}$$
Note that as $\omega t$ goes from $0$ to $\pi$ (i.e., the first one-half revolution), $\phi'$ goes from $\pi$ to $0$. And when $\omega t$ goes from $\pi$ to $2\pi$ (i.e., the second one-half revolution), $\phi$ goes from $\pi$ to $0$ again. Therefore, using $(5)$ we can write $\phi$ in terms of $\omega t$ as
$$\phi=\begin{cases}\pi -\omega t&,0\le \omega t<\pi\\\\2\pi-\omega t&,\pi<\omega t\le 2\pi \end{cases} \tag 6$$
Eliminating $\omega t$ from $(4)$ using $(6)$, we find that
$$\rho'=\begin{cases}R\left(\frac{\phi'}{\pi}\right)&,0\le \phi \le \pi \,\,\text{on first one-half revolution}\\\\R\left(1-\frac{\phi'}{\pi}\right)&,0\le \phi \le \pi \,\,\text{on second one-half revolution} \end{cases}$$
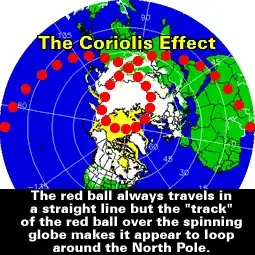 What is the equation of this loop?
The following image portrays a very similar image of a limacon
What is the equation of this loop?
The following image portrays a very similar image of a limacon
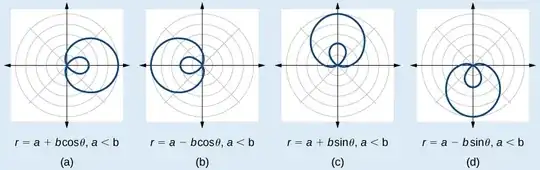 I am not really sure what approach to take on this problem:
Could parametric equations be used to solve this problem?
The parametric equations of a limacon can be found here: http://wiki.roblox.com/index.php?title=Parametric_equations#Lima.C3.A7on_trisectrix
I am not really sure what approach to take on this problem:
Could parametric equations be used to solve this problem?
The parametric equations of a limacon can be found here: http://wiki.roblox.com/index.php?title=Parametric_equations#Lima.C3.A7on_trisectrix