1

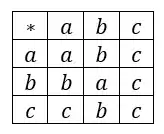
I understand what associativity is, and of course simple structures from elementary and high school mathematics like the natural numbers over addition are associative.

However, I think it would be clarifying to have an example of a mathematical structure that has almost no structure besides satisfying associativity, and that is also very simple.

user56834
  • 12,925

3 Answers3

2

Here are a couple of examples that involve very little structure.

The operation of catenation on digit strings from a fixed alphabet (numeric or otherwise).

The left forgetful operation defined by $a*b=b$ for any $a,b$ belonging to some fixed set.

(And, of course, the corresponding right forgetful operation.)

Dave L. Renfro
  • 36,843
1

If $X$ is any set, we can look at $$ \mathrm{Fun}(X) = \{f \mid f:X \to X\}. $$ This set is associative under composition. If $f,g,h \in \mathrm{Fun}(X)$, then $(f \circ g) \circ h = f \circ (g \circ h)$ because $$ ((f \circ g) \circ h)(x) = (f \circ g)(h(x)) = f(g(h(x))) = f((g \circ h)(x)) = f \circ (g \circ h)(x). $$ More generally, if you know what a homomorphism is, then you can also form $$ \mathrm{End}(X) = \{f\mid f:X \to X \text{ and $f$ is a homomorphism}\}. $$

Mees de Vries
  • 26,947
  • How would you use your notation $\operatorname{fun}$ to denote the set of functions between two different sets, say $A$ and $B$? I have seen the notation $B^A$, so would it be $\operatorname{fun}(A,B)$? – Alex Ortiz Sep 07 '16 at 19:48
  • I just made the notation up for this example. Actually, before I added the bit about homomorphisms, I used End in place of Fun. I changed it to avoid confusion between the specific and the general case. Since Fun is really a special case of End, I would ordinarily use End in place of Fun. Or indeed, use an exponential notation. – Mees de Vries Sep 07 '16 at 19:58
  • thanks for that. Where can I learn more about this notation? Including context? Seems like something that comes up somewhere in algebra. – Alex Ortiz Sep 07 '16 at 20:12
  • Uh, I suppose it would come up in algebra and more generally category theory. But it's really nothing deep or natural. – Mees de Vries Sep 07 '16 at 20:19
1

I hope the folllowing simple one is a typical one. Let $S = \{a, b, c\}$ and define the product $*$ as in the given table:

enter image description here

Then $S$ is a finite semigroup (which I think you are looking for). It satisfies associativity requirement: $$x * (y * z) = (x * y) * z$$ where $x,y$ and $z$ are arbitrary elements of set $S$. Note that $S$ is just closed under $*$ before having associativity.

Mikasa
  • 67,374
  • Yes, precisely I'm looking for a finite semigroup (I see that now after you suggested it). However, I'm looking for something intuitive. perhaps there is some intuitive semigroup that represents the rotation of a triangle or something visual/intuitive like that? – user56834 Sep 07 '16 at 19:44