2

I've asked questions about these problems before but thus far, no one has been able to help me understand. I've been attempting these problems for tens of hours over a couple of weeks now. I'm desperate for some help.

The problem are as follows:

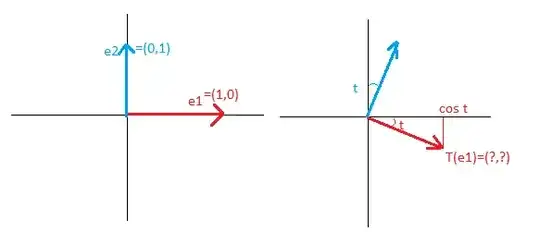
Exercise 6. Using the standard basis of $\mathbb R^2$, determine the matrix of each of the following linear transformations and compute their determinants:

(1) and anitclockwise rotation of angle $\theta$ around the origin.

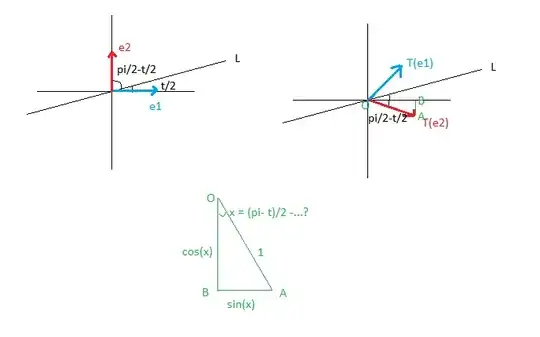
(2) (Harder) a reflection in a line forming an angle $\theta/2$ with the $x$-axis.

enter image description here

The issue is not the linear transformation aspects - I can do those problems well. However, despite having done trigonometry in the past, I think my professors skipped over anything comparable to this. I really just cannot grasp the trigonometry aspect of these. At this point, I've literally spent tens of hours trying to understand these and have not been able to. Please, help me understand how the trigonometry of these problems works and please use simple mathematical language.

Note that I have studied trigonometry in the past but there must be deficiencies since I just cannot understand how the trigonometric angles are derived using the usual ($x = \cos(\theta)$, $y = \sin(\theta)$).

According to the solutions given in the book the result should be $\begin{pmatrix} \cos\theta & \sin\theta \\ \sin\theta & -\cos\theta \\ \end{pmatrix}$.

Please help! I'm desperate at this point.

Thank you.

The Pointer
  • 4,182
  • Some related post (maybe you can find a few more): http://math.stackexchange.com/questions/1693200/find-a-matrix-for-the-linear-transformation-of-reflection-about-a-theta-line http://math.stackexchange.com/questions/1339305/how-to-find-the-standard-matrix-for-h%CE%B8-by-finding-the-images-of-the-standard-b http://math.stackexchange.com/questions/1715111/reflect-point-across-line-with-matrix – Martin Sleziak Sep 04 '16 at 05:50
  • And part 2 seems to be the same question as: http://math.stackexchange.com/questions/1913446/using-the-standard-basis-of-mathbbr2-determine-the-matrix-of-the-followin – Martin Sleziak Sep 04 '16 at 06:31

1 Answers1

2

Just give a sketch of what you want to do in your linear transformation! enter image description here

So can you determine the $T(e_1)$ and $T(e_2)$ using this figure and your basic trigonometry? Then you can to immediately write down the standard linear transformation matrix. I think this is not an issue for you from your problem description. But anyway I put down a link to my answer to a similar problem for reference: Sequence of rotation matrices

Now, for who is not quite familiar with the trig, we draw another figure to determine $T(e_1)$ in my figure using trigonometry. We construct a triangle ABC:

enter image description here

From the right-angled triangle definition, $sin(t)=\frac{opposite}{hypotenuse}$. We also have a pure rotation in this case. The length of the vector $T(e_1)$, which corresponds to segment $AB$ is $1$. Thus length of $BC$ is $sin(t)$. But the y coordinate of the end point of my $T(e_1)$ (red arrow) is $-sin(t)$, since the projection of this arrow to the y axis is pointing to the negative side (opposite to $e_2$). So we have $T(e_1)=(\cos t,-\sin t)$ in my drawing above.

Here is some extra hints for problem (2). Be careful of the angle between $T(e_1), T(e_2)$ and the horizontal axis though! enter image description here

Community
  • 1
Li Chun Min
  • 864