I have two functions whose functional forms are of Shannon entropy type. The functions are:
$$f_1 = x \log x + (1-x)\log (1-x)+y \log y + (1-y)\log (1-y)$$ and $$f_2 = xy \log (xy) + (1-xy)\log (1-xy).$$ Here both $x,y$ are less than 1.
Question: I want to know whether $f_2>f_1$ or $f_1>f_2$? Is there any inequality which says that. I tried some analytical calculation but couldn't succeed. Can anyone suggest anything?
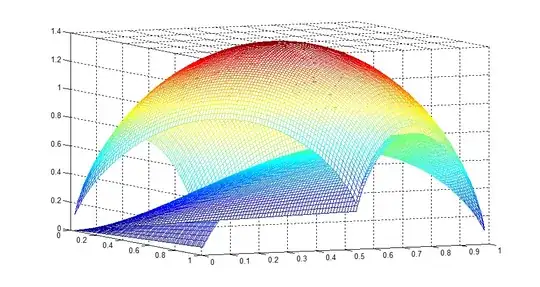
Let $\left(B_t\right)_{t\in[0,1]}$ be a family of independent random variables with $B_t$ being a Bernoulli random variable of parameter $t$ for every $t\in[0,1]$. Write $h(t)$ for the entropy (in the natural base $\text{e}$) $H\left(B_t\right)$ for all $t\in[0,1]$. Observe that $h:[0,1]\to\mathbb{R}_{\geq 0}$ is given by $$h(t)=-t\,\ln(t)-(1-t)\,\ln(1-t)$$ for all $t\in(0,1)$, and $h(0)=h(1)=0$.
Now, fix $x,y\in[0,1]$. First, note that $$H\left(B_xB_y\big|B_x\right)=x\cdot H\left(B_y\right)+(1-x)\cdot H\left(B_0\right)=x\cdot h(y)+(1-x)\cdot h(0)=x\cdot h(y)\,.$$ Thus, $$H\left(B_xB_y,B_x\right)=H\left(B_xB_y\big|B_x\right)+H\left(B_x\right)=x\cdot h(y)+h(x)\,.$$ On the other hand, $$H\left(B_xB_y,B_x\right)=H\left(B_x\big|B_xB_y\right)+H\left(B_xB_y\right)\geq H\left(B_xB_y\right)=H\left(B_{xy}\right)=h(xy)\,.$$ Consequently, $$h(xy)\leq x\cdot h(y)+h(x)\leq h(x)+h(y)\,.$$
The inequality $$h(xy)\leq h(x)+h(y)$$ for all $x,y\in[0,1]$ becomes an equality if and only if $x=1$, $y=1$, or $(x,y)=(0,0)$. Observe that $f_1=-\big(h(x)+h(y)\big)$ and $f_2=-h(xy)$, up to a positive scalar multiple (if you use a different logarithmic base $b>1$). Therefore, $f_1\leq f_2$.
A direct calculation shows that $f_1<f_2$ as given in the picture, where the two surfaces represent $-f_1, -f_2$ respectively for $0<x,y<1$.
Let $A$ and $B$ be independent Bernoulli random variables with parameters $x$ and $y$ respectively. Observe that $-f_1(x,y)=H(A,B)$ the entropy of the pair $(A,B)$, while $-f_2(x,y)=H(A\land B)$ the entropy of the logical conjunction of $A$ and $B$. Clearly, $H(A,B)>H(A\land B)$ for $0<x,y<1$ (why?). Therefore, $f_2(x,y)>f_1(x,y)$ for $0<x,y<1$.
