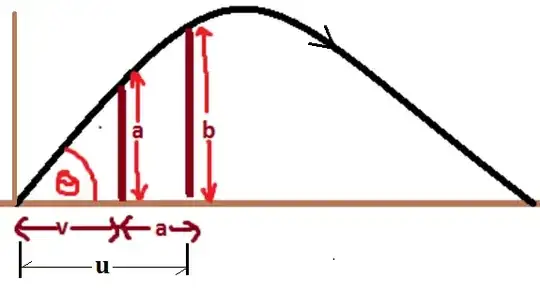
An object which is projected from the ground with an angle of $\theta$ passes two walls(without touching) within its motion.The wall which has a height of 'a' is situated in a distance of 'v' from the projected place and the other wall which has a height of 'b' is situated in a distance of 'a' from the first wall. Find a expression with a and b for the $\tan$ value of the $\theta$.
I tried to find the $\theta$,
$\rightarrow s = ut \\ v=u\cos\theta.t_{1}\\$
$\uparrow s=ut+\frac{1}{2}at^{2}\\ a=u\sin\theta\times\frac{v}{ucos\theta}-\frac{g}{2}\times\frac{v^{2}}{u^{2}\cos^{2}\theta}\\ a=v \tan\theta-\frac{gv^{2}\sec^{2}}{2u^{2}}$
$\rightarrow s=ut\
v+a = u\cos\theta\times t_{2}$
$\uparrow s=ut+\frac{1}{2}at^{2}\\ b=u\sin\theta\times\frac{v+a}{u\cos\theta}-\frac{g}{2}\times\frac{(v+a)^{2}}{u^{2}\cos^{2}\theta}\\ b=(v+a)\tan\theta-\frac{g(v+a)^{2}\sec^{2}\theta}{2u^{2}}$
I don't see a way to find the $\theta$.Please help.