What equation can produce these curves?

Question

Does an equation exist that can produce the curves shown in the attached image, by varying a single variable?

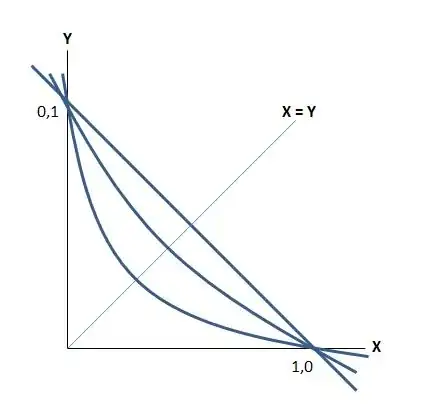
enter image description here

Do you mean in principle, or are you asking for specific examples? — Christopher King, Jul 05 '16 at 03:17

score 10 · Accepted Answer · 2016-07-05T07:47:08.193

10

Consider the equilateral hyperbola $xy=1$ and map the points $(1,0)$ and $(0,1)$ to two symmetrical points on the hyperbola $(t,t^{-1})$ and $(t^{-1},t)$ by translation/scaling (as if you were zooming in).

$$(x(t-t^{-1})+t^{-1})(y(t-t^{-1})+t^{-1})=1.$$

The straight line corresponds to two infinitely close points, $t=t^{-1}=1$, which is a degenerate case of the equation.

Previous answer:

You can think of a pencil of parabolas, $y=\frac1{\sqrt2}+\frac\lambda{\sqrt2}(2x^2-1)$, which you rotate by $45°$ right, giving

$$x+y=1+\lambda\left((x-y)^2-1\right).$$

You can solve the quadratic equation for $y$.

edited Jul 05 '16 at 07:47

answered Jul 04 '16 at 21:41

1

If I take $(x,y)$ to be $(1,0)$ or $(0,1)$, it seems to me that your equation is not satisfied. – Jeppe Stig Nielsen Jul 04 '16 at 21:51
1

@JeppeStigNielsen: right, I forgot a $\sqrt2$ factor. Now fixed (hopefully). – Jul 04 '16 at 22:11
This has become promising, since the it goes through the two points as required, and is has the symmetry that swapping $x$ and $y$ leaves the equation unchanged. However for some values of $\lambda$ it may look different than expected. Like when $\lambda$ is close to $1$, the vertex of the parabola is close to the origin, and the parabola (after rotation) crosses the coordinate axes in the "opposite" direction, I think. – Jeppe Stig Nielsen Jul 04 '16 at 22:34
@JeppeStigNielsen: the exponent $2$ can be lessened, but at some point we are lacking curve specifications. – Jul 04 '16 at 22:36
At what value of $\lambda$ will the two axes be tangents at the two "fixed" points? – Jeppe Stig Nielsen Jul 04 '16 at 22:40
Your current image "before rotation" is also magnified by a factor $\sqrt{2}$ compared to the image of the question. The biggest isosceles right triangle has side lengths $1,1,\sqrt{2}$ in the correct solution, and side lengths $\sqrt{2},\sqrt{2},2$ in the current image of this answer. One can easily confuse oneself with this. However, your formula $$x+y=1+\lambda\left((x-y)^2-1\right)$$ is good, as I said, because it is symmetric in swapping $x$ and $y$ and is correct for $(1,0)$ and $(0,1)$. It might still be interesting to see another family of curves, maybe hyperbolas instead of parabolas. – Jeppe Stig Nielsen Jul 04 '16 at 22:54
The plot does not correspond to the equation, I removed it. – Jul 04 '16 at 22:57

Narasimham · Answer 2 · 2016-07-05T15:02:18.603

Assuming what you drew to be a parabola, and $p$ a constant to push each parabola along the line of symmetry,

$$ y = p (1-x^2) $$

Now rotate them clockwise by $\pi/4 \, , (x,y) \rightarrow ( x+y, x-y)/\sqrt2. $

EDIT1:

As you left it free as regards shape within constraints, we could use a cosh curve, sec curve etc.

In fact, we can generalize this using any open even function E(x) , passing through $(\pm 1/\sqrt{2},1/\sqrt{2} ). $

Letting

$$y(x,p) = (1 + p *(1/2 - x^2) E(x)) /\sqrt{2} \, $$

and building a differentiable function, rotating the curve by $-\pi/4$, we can make the family pass through singular points $(0,1),(1,0) $as shown above and illustrated below in a particular case.

In graph below $E(x) = \cos^2(x) $is chosen with $ p= (\pm 2,0). $

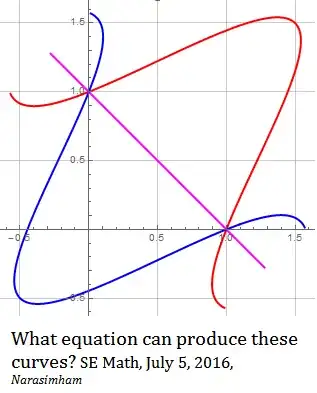
For the earlier special case you got parabolas using $E(x)=1 $ perturbed by arbitrary $p$ values.

score 2 · Answer 3 · answered Jul 04 '16 at 21:48

2

Try a superellipse: $|x|^a + |y|^a =1$ with $0 <a \le 1$.

answered Jul 04 '16 at 21:48

lhf

216,483

3

Yes, but that curve will not intersect (pass through) the coordinate axes and continue into the 2nd/4th quadrant as shown in the image. But maybe that was not a requirement. – Jeppe Stig Nielsen Jul 04 '16 at 22:02
@JeppeStigNielsen You could try analytic continuation, or simply remove the $|\cdot|$ – Tobias Kienzler Jul 05 '16 at 06:01
@TobiasKienzler The superellipse with $a<1$ has a cusp at the point in question. It is not meeting the axis at a non-zero angle like in the drawing of the question. – Jeppe Stig Nielsen Jul 05 '16 at 09:11
@JeppeStigNielsen Right you are, I spoke to soon... – Tobias Kienzler Jul 05 '16 at 09:50

lhf · Answer 4 · 2016-07-05T00:41:39.670

2

Try also a quadratic Bézier curve $$ \gamma(t) = (1 - t)^{2} P_0 + 2(1 - t)t P_1 + t^{2} P_2 $$ where $P_0=(1,0), P_1=(a,a), P_2=(0,1)$, with $a \in [0,0.5]$.

edited Jul 05 '16 at 00:41

answered Jul 05 '16 at 00:36

lhf

216,483

score 2 · Answer 5 · answered Jul 05 '16 at 06:00

You can first of all use a tool such as Engauge Digitizer to obtain tables of data points for each curve. Then either try a Log-log plot to determine a polynomial approximation or use a fitting tool of your choice to obtain fits of the same kind for each curve. Finally, find a parameter describing each curve such that all the fit-parameters previously obtained can also be fitted by simple functions, ideally linear or a low-order polynomial.

score 0 · Answer 6 · answered Jul 05 '16 at 07:58

Use Lagrange Interpolation formula: For a variable point $(t,t)$ on the line $x-y=0$ with $0<t\leq \sqrt2/2$, fit a degree 2 polynomial curve that passes through the three points $(0,1), (t,t)$ and $ (1,0)$.

For $t=\sqrt2/2$ the three points will be collinear and it will automatically give a straight line. This must produce the same result as Yves Daoust's answer above, but using different interpretation.

What equation can produce these curves?

6 Answers6

Linked