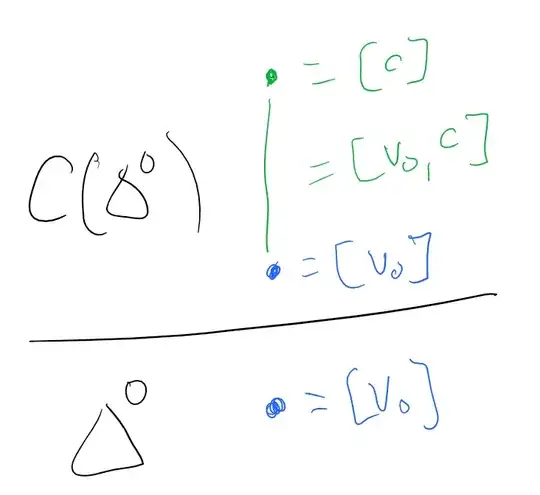Here are some thoughts that could hopefully help.
First of all, trying to give the product of two simplices a simplicial (or $\Delta$-complex) structure is in general annoying. There's a reason that the relevant sections of Hatcher are rather technical (see for example the proof of Theorem 2.10 - page 112 here (PDF)).
Here's one thing that is neat about simplices (when I say simplices I mean $\Delta$-complexes but I'm being sloppy) though, and this construction actually underlies a lot of what you're doing.
Let's suppose that $\sigma = [v_0, \cdots, v_n]$ is an $n$-simplex. Then it has an $(-1)^n$-oriented codimension-1 face $\tau = [v_0, \cdots, v_{n-1}]$, and this is just an $(n-1)$-simplex.
Now let's add a point $v_{n+1}$ to everything - just put it at the end of every simplex. We boost $\sigma$ to an $(n+1)$-simplex $\tilde{\sigma} = [v_0, \cdots, v_n, v_{n+1}]$. And now it has an $(-1)^n$-oriented face $\tilde{\tau} = [v_0, \cdots, v_{n-1}, v_{n+1}]$ which is still codimension-1, and this is just an $n$-simplex.
This is actually super-neat. Let's suppose we have a description of a space $X$ realized as a collection of simplices $\{\sigma_i\}$. Then a simplicial description of $CX$ is given by $\{\sigma_i, [c], \tilde{\sigma}_i\}$, where $\tilde{\sigma}_i$ just denotes adding $c$ to the end of the list of vertices of $\sigma_i$.
If you want to see some poorly-drawn examples, here you go:
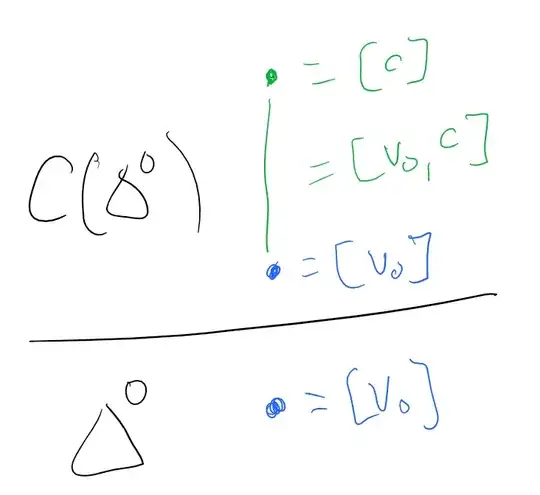
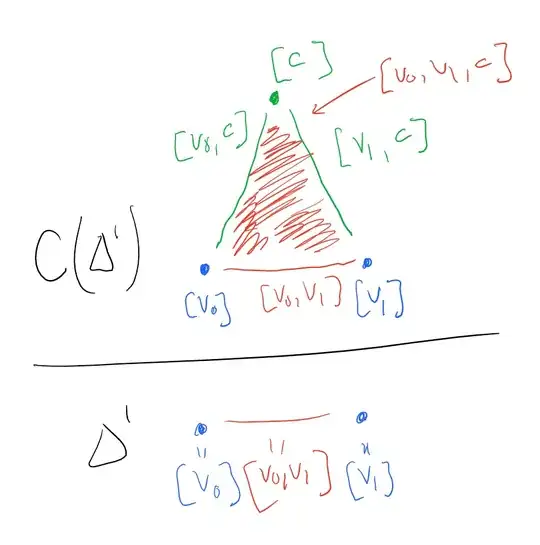
Hopefully these convince you that $C(\Delta^n) = \Delta^{n+1}$.
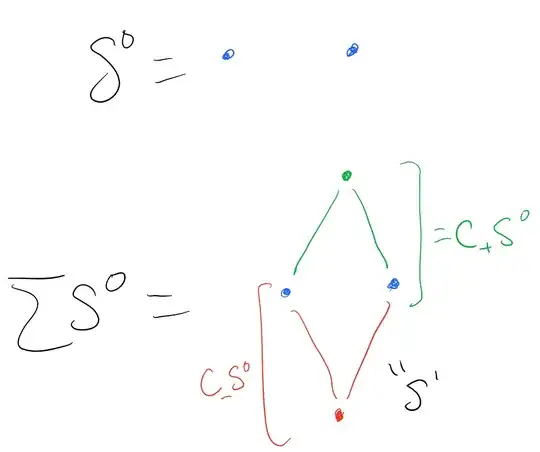
For the suspension, there's a really important point that your notation makes it unclear whether you get it. So I'll say it, and you may well already know it. You identify $Y \times \{0\}$ to one point, and $Y \times \{1\}$ to a different point. Otherwise the equality $\Sigma S^n = S^{n+1}$ wouldn't be true.
Perhaps it's better to think about the suspension as two cones smushed together. Given a space $X$ we can form cones $C_+X$ and $C_-X$, and these come with canonical inclusions $X \to C_{\pm}X$. Then the suspension is just the union of $C_+X$ and $C_-X$ with the two copies of $X$ identified. In the case of the sphere, these correspond to the north and south hemispheres.
In particular, if we start off with $S^0$ as two points (0-simplices), then $S^1 = \Sigma S^0$ is four 1-simplices, one for each quadrant in the standard embedding $S^1 \to \mathbb R^2$, $S^2 = \Sigma S^1$ is eight 2-simplices, one for each octant in $\mathbb R^3$, and so on and so forth.
If you want another poorly-drawn picture, here you go: