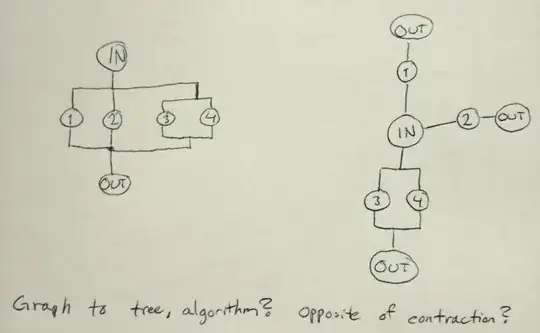
The graph has tree paths IN-1-OUT, IN-2-OUT and IN-3&4-OUT between IN and OUT in the left. I want to make each path to a branch like the right.
What is the name of this operation or the name of this procedure to make a graph into a tree?
Asked
Active
Viewed 150 times
0
hhh
- 5,469
1 Answers
0
Not tree unless changes such as changing the OUT vertices or removing paths
This picture below does not represent a tree because
"a tree is an undirected graph in which any two vertices are connected by exactly one path."
where you have many paths between IN vertex and OUT vertex. You could call different OUT vertices with OUT1, OUT2 and OUT3 -- similarly for paths IN-3-OUT and IN-4-OUT so each parallelization increases the number of OUT vertices by one.
Operations to make the graph to tree
The name of the operations contain insertion of vertices and removal/insertion of edges as written in the picture. Other way to see this is to consider graph theory in terms of linear algebra. So
the path matrix $P_{in}$ where $in$ is the root is {{1, out}, {2,out}, {3,out}, {4,out}} while the reduced path matrx $P_{in}^{-1}$ is {{1}, {2}, {3}, {4}} with the last out-edge removed.
Path matrix $P_n$ representation for graph $G$ where $n$ is a root vertex. The $j$th column is a path such that the entry is 1 if the edge in the path and 0 otherwise. (Page 17 of Graphs And Matrices by Babat 2nd ed)
