First of all, & looking at the suggested question list, I hesitate at asking this basic question:
Here goes. I'm trying to assess my fitness, and I need a bit of mathematical help. I do a little jogging, along many paths around my very hilly neighbourhood, at different times of year, so the routes aren't comparable - I need to adjust for the hills.
I tap out each route on Google Earth, from which I obtain distance, and total metres of ascent and of descent.
Ascent slows you down, & a metre of ascent can be replaced by A metres of distance. Descent is a bit more uncertain - it speeds you up if very gentle, and slows you if steep. So replace a metre of descent with D linear metres. So I can calculate an adjusted distance, and so an adjusted time per mile.
I thought at first that changing A and D until I got a minimal standard deviation for all the adjusted mile times would best remove the effect of the hills. But since smaller times makes for a smaller SD the minimum was nonsense: when I got there A & D were both large positives, and so I seemed to move at Olympic speed.
So I introduced a 3rd constant C to add seconds to all the route times, and adjusted all 3 until I had a minimum SD when net-downhill route times had been lengthened by the adjustments, and net-uphill ones shortened.
so minimize SD of all the: (time + C) / (linearmetres + ascentmetres * A + descentmetres * D)
Result: 1 metre uphill = +8 metres of flat. 1 metre downhill = +3m of flat. (It's positive because the hills are steep and my knees are shot.)
What I want to ask is: Is there a way to optimise this without involving the 3rd constant? Because it seems like a subjective adjustment. What kind of maths should I be using?
sadly no graph of pre-adjustment times (blue) and post-adjustment is allowed..
[edit: somehow I now have 11 reputation points, so..]
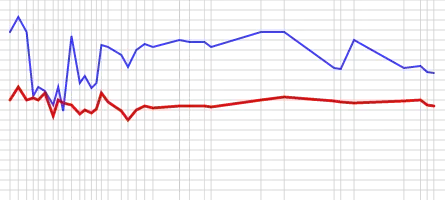Thanks for reading.
