The sign of the Gaussian curvature can be used to classify points as elliptic, hyperbolic, and parabolic. Wikipedia has this image with example surfaces:
I see how a hyperboloid surface has hyperbolic points, and respectively a sphere or ellipsoid has elliptic points. So these are aptly named.
But why are points with zero Gaussian curvature named parabolic, not something like cylindrical or conical? Especially, a paraboloid has positive curvature.
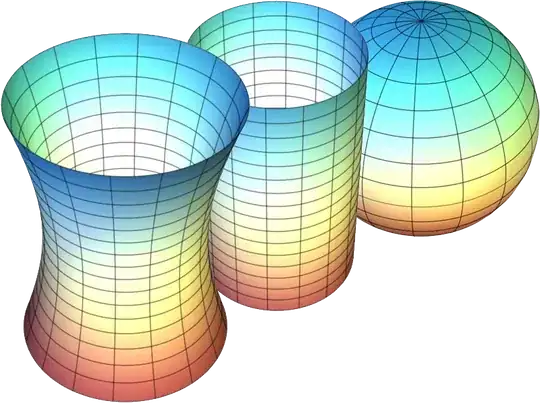
Nomenclature is from origin of conics categorization . Among the conics eccentricity $\epsilon$ for a hyperbola, parabola and ellipse are $ \gt 1, = 1, \lt 1 $ respectively. In its categorizing work sign of double or Gauss curvature relates to $ (1- \epsilon). $
In the equation of conic( two dimensions) there is already an indicator of things to come when it would be embedded in 3-space. For $ a x^2 + 2 h x y + by^2 $ + linear terms =0, then the sign of invariant $ a \cdot b - h^2 $ also decides to which of the three types the conic under consideration belongs.
Accordingly in $ \mathbb R^{2}$ say for a surface in Monge form $ z= f(x,y), K= (r \cdot t - s^2)/(1+p^2+q^2)^2 $ (partial derivatives of z) decides sign of Gauss curvature K, i.e., to which of the three types you have shown the surface belongs.
EDIT 1:
Also if a reputed mathematician had called it that way and it stuck,the matter of distinguishing between the three was settled temporarily.
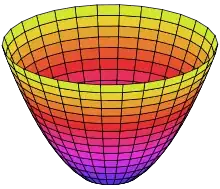
Having said the above in defense of what I believe is the staus quo ante I am in agreement with the OP about inappropriateness of the parabolic appellation of $ K=0 $ flat surfaces.
When a paraboloid is and quite apparently looks $K >0$ there is no need to cling on to any historical reasons. In line with the view of OP I too like to see it changed to developable or flat, but not further retain parabolic.
