1

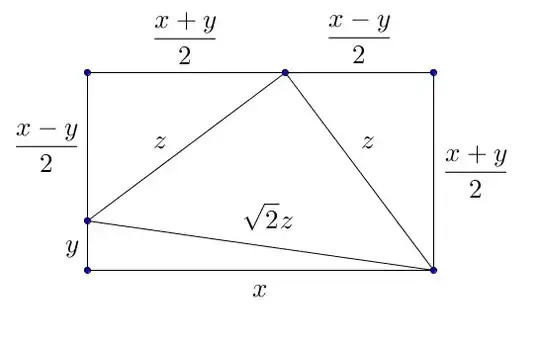
I'm told that if $r^2 + s^2 = z^2$ then $(r+s)^2 + (r-s)^2 = 2z^2$, which is obvious. But i'm trying to show that every integer solution to $x^2 + y^2 = 2z^2$ arises this way from a Pythagorean Triple (r,s,z) and then go on to find the general solution of $x^2 + y^2 = 2z^2$ where $gcd(x,y,z)=1$.

I started by saying that $a,b \in \mathbb{Z}$ was an integer to solution to $x^2 + y^2 = 2z^2$, then $a^2 + b^2 = 2z^2$ and then trying to show that there exist some $a_1 , b_1$ such that $a = a_1 + b_1$, $b=a_1 - b_1$, but i haven't seem to have gotten anywhere. I find myself going in circles. Any tips?

gsins
  • 13

3 Answers3

2

This picture shows the correspondence between Pythagorean triangles and $x^2 + y^2 = 2z^2$ triangles. Note that, if $x^2 + y^2 = 2z^2, $ then $x$ and $y$ are either both even or both odd. In either case $\frac{x+y}{2}$ and $\frac{x-y}{2}$ are both integers.

two to one

Steven Alexis Gregory
  • 26,769
1

From $a^2+b^2=2z^2,$ assuming $a\ge b,$ if you want $a=a_1+b_1,\ b=a_1-b_1$ then $a_1=(a+b)/2$ and $b_1=(a-b)/2.$ Here you need then to require that $a,b$ have the same parity to be able to do this manipulation.

Note: If one already has $a^2+b^2=2z^2$ then the requirement mentioned above, that the parity of $a,b$ are the same, is implied (an odd square plus an even square would be odd, not $2z^2.$)

An example: $1^2+7^2=2\cdot 5^2,$ and then $(7+1)/2=4,\ (7-1)/2)=3.$ This then goes with $4^2+3^2=5^2.$ So I can see your method will generate Pythagorean triples. SOme care may need to be taken to make sure one ends up with primitive triples.

Added explanation: Starting from $$x^2+y^2=2z^2\tag{*}$$ in which we may assume $\gcd(x,y,z)=1$ and $x \ge y$ for definiteness, we have $x,y$ odd and so may define $r=(x+y)/2,\ s=(x-y)/2.$ Then $$r^2+s^2=(1/2)(x^2+y^2)=(1/2)(2z^2)=z^2.$$ So we do have the solution to $(*)$ arising from a Pythagorean triple $(r,s,z)$ as required.

coffeemath
  • 29,884
  • 2
  • 31
  • 52
  • See this. – Steven Alexis Gregory Jun 02 '15 at 00:58
  • @StevenGregory I found your answer to the other question interesting, [Likely I'll upvote that once I get a chance to go through it better], although a bit involved as a response to this particular question from user gsins. I've added a bit of explanation to my rather obvious answer detailing only how to get the Pythagorean triple from a given solution to $x^2+y^2=2z^2.$ – coffeemath Jun 02 '15 at 02:31
0

In General, for the equation;

$$x^2+y^2=az^2$$

If you can represent a number as a sum of squares. $a=t^2+k^2$

The solution can be written in this form.

$$x=-tp^2+2kps+ts^2$$

$$y=kp^2+2tps-ks^2$$

$$z=p^2+s^2$$

For the case:

$$x^2+y^2=2z^2$$

Solutions will be:

$$x=-p^2+2ps+s^2$$

$$y=p^2+2ps-s^2$$

$$z=p^2+s^2$$

$p,s - $any integer.

individ
  • 4,301