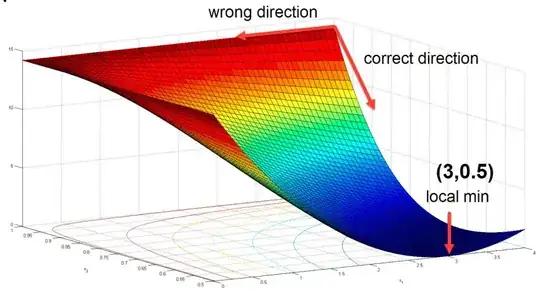
In the newton optimization algorithm to find the local minimum $x^*$ of a non-linear function $f(x)$ with iteration sequence of $x_0 \rightarrow x_1 \rightarrow x_2 ... \rightarrow x^*$ all $\nabla ^2 f(x_k)$ should be pos. definite otherwise search direction might not be a descent direction. The solution to this problem is to use Hessian modification techniques.
I am looking for a simple function that has local minimum at $x^*$, but $\nabla ^2 f(x_k)$ is not positive definite, and hence the Newton algorithm fails. Then after using one of the Hessian modification techniques, Newton algorithm converges to $x^*$