We know that the odd terms of Dirichelt Beta function are $\frac{\pi }{4}$,$\frac{\pi^3 }{32}$,$\frac{5\pi^5 }{1536}$,... If we use the WolframAlpha to find the limit of the odd terms only divided by $n$ when the $N\rightarrow \infty $ as shown in below equation
$$\lim_{N\rightarrow \infty }\sum_{n=1}^{N }\frac{\beta (2n-1)}{n}$$
The results of WolframAlpha were as shown below
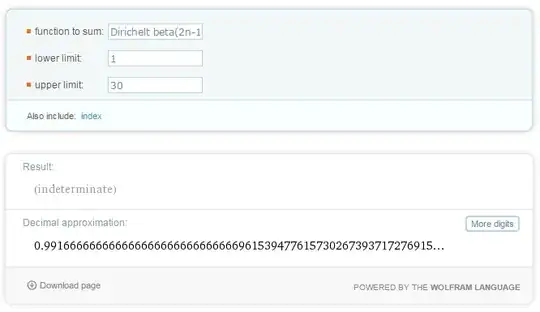
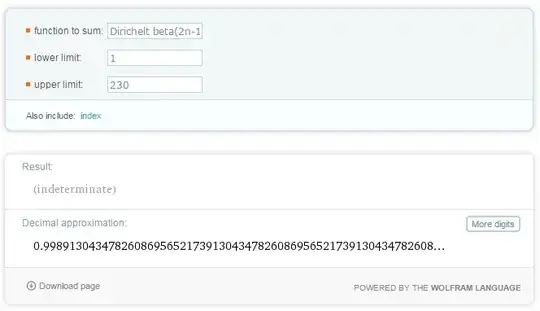
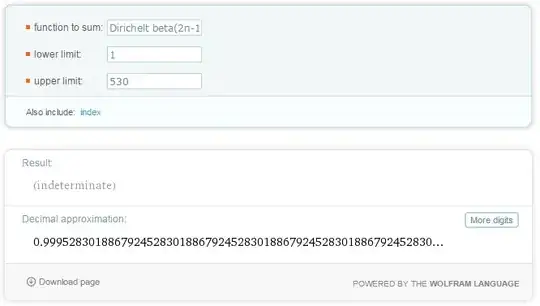 we see the limit go to $1$
we see the limit go to $1$
But if we take the limit for all terms (add and even) as shown below $$\lim_{N\rightarrow \infty }\sum_{n=1}^{N }\frac{\beta (n)}{n}$$ the result become
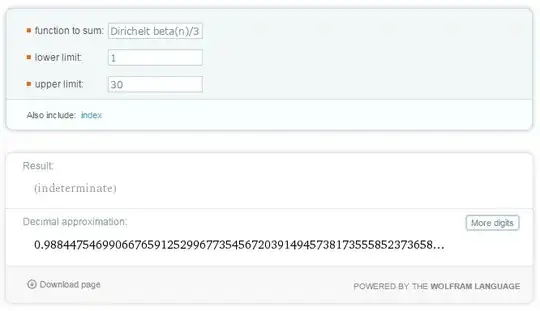
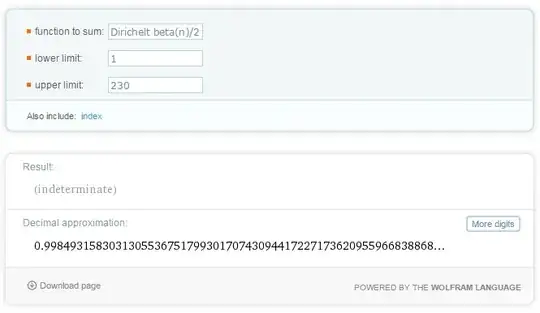
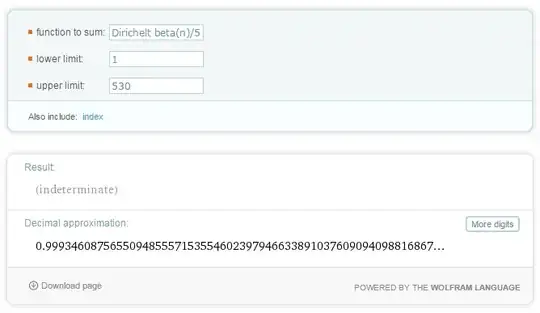
I cannot continue for more $n$ because the ability of Wolfarm stopped up to $n=550$
We see the limit also go to $1$
My question is "Which limit will give $1$"