How to find ring of coverage of GPS Satellite on WGS-84 ellipsoid?

Question

Given the following:

1. Time, t
2. The set of IS-200 Ephemeris data, E, of a GPS Satellite corresponding to time t
3. The ECEF position of the GPS satellite, P=(x,y,z), derived from the time and ephemeris, (t,E).
4. Assume the earth is just the WGS-84 ellipsoid.
5. All points on WGS-84 have the mask angle, m.

Find the following:

1. the ring of coverage, R, on WGS-84 of the GPS satellite. i.e., the boundary which distinguishes which WGS-84 points are in view the satellite at point P=(x,y,z) and which WGS-84 points are not in view

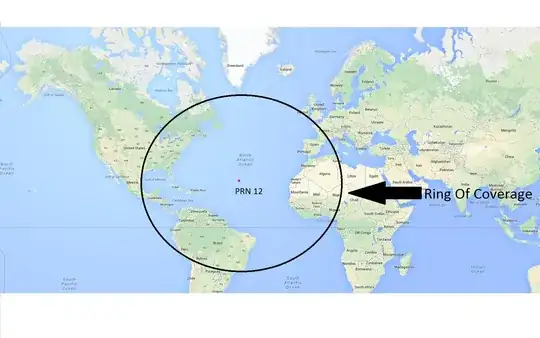
Acceptable solutions:

1. A spline over WGS-84 that approximates R.
2. A polygon over WGS-84 that approximates R.
3. Or a formula(s) that gives me R.

What I have tried so far:

• Let e^2 = 0.0066943799901264; eccentricity squared

We have a ECEF WGS-84 position by geodetic latitude phi and longitude lambda:

r = 1/(sqrt(1-e^2 sin^2(phi))) * (cos(phi)*cos(lambda), cos(phi)*sin(lambda), (1-e^2) * sin(phi))

I then convert ECEF to east-north up (ENU) geographic frame with phi and lambda using the matrix:

     (-sin(lambda)                  cos(lambda)                  0       )
C=   (-cos(lambda)*sin(phi)        -sin(lambda)*sin(phi)         cos(phi))
     ( cos(lambda)*cos(phi)         sin(lambda)*cos(phi)         sin(phi))

• Let G = C ( P - r )
• Take the z component of G. should the z component of G be greater than sin(m) then I know the point, r, is in view. But that isn't sufficient get the solution that I am after. I could just find a bunch of points that are in view and take the convex hull of those points, but that is not efficient at all.

Answer 1

The solution for an ellipsoid is pretty messy--it is an irregular shape, not a circle--and is best computed numerically rather than with a formula.

On a world map the difference between the WGS84 solution and a purely spherical solution will only barely be noticeable (it's about one pixel on a screen). The same difference would be created by changing the mask angle by about 0.2 degrees or in using a polygonal approximation. If these errors are acceptably small, then you can exploit the symmetry of the sphere to obtain a simple formula.

This map (using an Equirectangular projection) shows the coverage for a satellite at 22,164 kilometers (from the earth's center) with a mask angle of m = 15 degrees on the WGS84 spheroid. Recomputing the coverage for a sphere does not visibly change this map.

On the sphere, the coverage will truly be a circle centered at the satellite's location, so we only need to figure out its radius, which is an angle. Call this t. In cross-section there is a triangle OSP formed by the earth's center (O), the satellite (S), and any point (P) on the circle:

• The side OP is the radius of the earth, R.

• The side OS is the height of the satellite (above the earth's center). Call this h.

• The angle OPS is 90 + m.

• The angle SOP is t, which we want to find.

• Because the three angles of a triangle sum to 180 degrees, the third angle OSP must equal 90 - (m + t).

The solution is now a matter of elementary trigonometry. The (planar) law of sines asserts that

sin(90 - (m+t)) / r = sin(90 + m) / h.

The solution is

t = ArcCos(cos(m) / (h/r)) - m.

As a check, consider some extreme cases:

1. When m = 0, t = ArcCos(r/h), which can be verified with elementary Euclidean geometry.

2. When h = r (the satellite hasn't launched), t = ArcCos(cos(m) / 1) - m = m - m = 0.

3. When m = 90 degrees, t = ArcCos(0) - 90 = 90 - 90 = 0, as it should be.

This reduces the problem to drawing a circle on the sphere, which can be solved in many ways. For instance, you can buffer the satellite's location by t * R * pi/180 using an equidistant projection centered at the satellite. Techniques for working with circles on the sphere directly are illustrated at https://gis.stackexchange.com/a/53323/664.

---

Edit

FWIW, for GPS satellites and small mask angles (less than 20 degrees or so), this non-trigonometric approximation is accurate (to a few tenths of a degree and less than a few hundredths of a degree when the mask angle is under 10 degrees):

t (degrees) = -0.0000152198628163333 * (-5.93410042925107*10^6 + 
              3.88800000000000*10^6 r/h + 65703.6145507725 m + 
              9.86960440108936 m^2 - 631.654681669719 r/h m^2)

For example, with a mask angle of m = 10 degrees and a satellite at 26,559.7 km above the earth's center (which is the nominal distance of a GPS satellite), this approximation gives 66.32159..., whereas the value (correct for the sphere) is 66.32023... .

(The approximation is based on a Taylor series expansion around m = 0, r/h = 1/4.)