How can easily I convert polar coordinates (using an arbitrary location as the "pole") into latitude and longitude in Google Earth Engine?

Question

Let's say I have an arbitrary point marked by WGS84 lat/lon. From that point, I measure the distance (in meters) and direction (as an absolute bearing from true north) from that waypoint to the nearest tree.

What is the lat/long of the tree?

Note: pretend I'm not interested in the mathematics of spherical geometry, which is well-covered in this question. I just want an answer. Also, I actually have hundreds of locations and thousands of trees, and I want the coordinates of those trees yesterday. You're going to do it for me, in the software you're familiar with. How are you doing it?

For example, if the waypoint's location is -119.99520, 39.51003 and the relative polar coordinate of nearest tree is 8.0 meters away at a heading of 210°.

Some possible answers using Arc and QGIS. How can this be done in Earth Engine?

What is wrong with the spherical world? You know the radius of Earth and I guess that with a distance of 8 meters the error due to using a spherical approximation is small. — user30184, Oct 23 '23 at 05:53
You need to restrict your question to a single software system only. This means if anyone else wants to find the answer to your question and only has that system, then if this Q is flagged as answered they will find their answer here. If you really want the answer for several systems, ask several questions and put the name of the software in the title as well as the tags. — Spacedman, Oct 23 '23 at 05:57
If you want to ask a general question about the "best" way to calculate the coordinates, leave out any reference to specific software. — Spacedman, Oct 23 '23 at 05:58
Good suggestions, @Spacedman. I've edited the question to narrow the scope. — Anson Call, Oct 23 '23 at 20:21

Oliver Lopez · Accepted Answer · 2023-10-23T08:15:25.440

You would need to specify a projection in which to work so that you can transform the point, add the respective delta X and delta Y in meters, then you can transform it back to lon/lat. Here's how you can do it in Google Earth Engine:

function ptFromBearing_euclidean(pt, d, brng, proj, maxError){
  /* Pt from bearing in Euclidean space
   pt: the point in lon,lat (EPSG:4326)
   d: distance in meters
   brng: bearing from North, in degrees
   proj: Projection in which to calculate the distance
  */
  var lon = ee.Number(pt.coordinates().get(0));
  var lat = ee.Number(pt.coordinates().get(1));
  var D2R = ee.Number.expression("Math.PI/180")
brng = ee.Number(brng);
  d = ee.Number(d);
  var deltaY = ee.Number.expression(
    "rsin(a)",
    {r:d, a:ee.Number(90).subtract(brng).multiply(D2R)})
  var deltaX = ee.Number.expression(
    "rcos(a)", {r:d, a:ee.Number(90).subtract(brng).multiply(D2R)}

  )
  var pt2 = pt.transform(proj,maxError)
  var pt2Coords = pt2.coordinates()
  var eX = ee.Number(pt2Coords.get(0))
  var eY = ee.Number(pt2Coords.get(1))
  return ee.Geometry.Point([eX.add(deltaX), eY.add(deltaY)],proj)
  .transform(ee.Projection("EPSG:4326"))
}

for the spherical case, no need to specify projection:

function ptFromBearing_spherical(pt, d, brng){
  /* Pt from bearing in spherical coordinates
   pt: the point in lon,lat (EPSG:4326)
   d: distance in meters
   brng: bearing from North, in degrees
  */
  var lon = ee.Number(pt.coordinates().get(0));
  var lat = ee.Number(pt.coordinates().get(1));
brng = ee.Number(brng);
  d = ee.Number(d);
  var R = ee.Number(6371*1e3);
  var D2R = ee.Number.expression("Math.PI/180")
var sinLat = ee.Number.expression(
  "sin(lat)cos(d/R) + cos(lat)sin(d/R)cos(brng)",
  {lat:lat.multiply(D2R), brng:brng.multiply(D2R), d:d, R:R})

  var y = ee.Number.expression(
    "sin(brng)sin(d/R)cos(lat)",
    {lat:lat.multiply(D2R), brng:brng.multiply(D2R), d:d, R:R.multiply(D2R)})
  var x = ee.Number.expression(
    "cos(d/R)-sin(lat)sinLat2",
    {lat:lat.multiply(D2R), sinLat2:sinLat, d:d, R:R})
  var lon2 = ee.Number.expression(
    "lon + deltaLon",
    {lon:lon, deltaLon:x.atan2(y)})
  var lat2 = sinLat.asin().divide(D2R)
return ee.Geometry.Point(lon2,lat2)
}

Here's how you would apply it to your example point in your question:

var d = 8 // distance in meters
var brng = 210 // Bearing (degrees) from North 
var pt = ee.Geometry.Point( -119.99520, 39.51003)
var ptSph = ptFromBearing_spherical(pt, d, brng)
var maxError = 0.1
var proj = ee.Projection("EPSG:3857")
var ptEuc = ptFromBearing_euclidean(pt, d, brng, proj, maxError)

and here's how it looks like in a map:

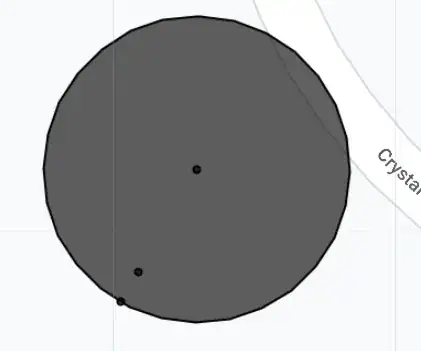
The circle around the original point was done by expanding the original point by a buffer of 8 meters, which by default works in a spherical coordinate system. You can see that one of the points (ptSph) lies in the perimeter of this circle, while the other one (ptEuc) is not.

The code below shows this example, as well as how to apply it to an arbitrary feature collection consisting of points, each with its own distance and bearing parameters.

https://code.earthengine.google.com/d85048c8f50397f0ba2ecdd9cd9d5c44

var randomPts = ee.FeatureCollection.randomPoints(geometry, 10)
randomPts = randomPts.randomColumn("distance").randomColumn("bearing").map(function(x){
  var distance = ee.Number(x.get("distance")).multiply(10) // from 0 to 10 m distance.
  var bearing = ee.Number(x.get("bearing")).multiply(360) // from 0 to 360 degrees.
  return x.set({distance:distance, bearing:bearing})
})
var randomPtsSph = randomPts.map(function(x){
  var pt = x.geometry()
  var d = x.get("distance")
  var b = x.get("bearing")
  var pt2 = ptFromBearing_spherical(pt,d,b)
  return ee.Feature(pt2, null)
})
var randomPtsEuc = randomPts.map(function(x){
  var pt = x.geometry()
  var d = x.get("distance")
  var b = x.get("bearing")
  var pt2 = ptFromBearing_euclidean(pt, d, brng, proj, maxError)
  return ee.Feature(pt2, null)
})

How can easily I convert polar coordinates (using an arbitrary location as the "pole") into latitude and longitude in Google Earth Engine?

1 Answers1