Smoothing corners in polyline using PyQGIS

Question

I have an array of QgsPointXY that makes a line with lots of vertices.

How can I round the corners?

Here is what I mean:

The code is:

def __round(line: list[QgsPoint], radius: float) -> QgsGeometry:
        rounded_line = QgsGeometry()
    for i in range(len(line) - 2):
        # Get the start and end points of the line segment
        start_point = line[i]
        end_point = line[i + 1]

        # Calculate the midpoint between the start and end points
        mid_point = QgsPoint(
            (start_point.x() + end_point.x()) / 2, (start_point.y() + end_point.y()) / 2)

        # Calculate the direction angle of the line segment
        direction_angle = start_point.azimuth(end_point)

        # Calculate the perpendicular angle to the direction angle
        perpendicular_angle = direction_angle + 90

        # Convert the perpendicular angle to radians
        perpendicular_angle_radians = perpendicular_angle * 3.14159 / 180

        # Calculate the center of the circular arc
        center_point = QgsPoint(mid_point.x() + radius * math.cos(perpendicular_angle_radians),
                                mid_point.y() + radius * math.sin(perpendicular_angle_radians))

        # Calculate the start and end angles of the circular arc
        start_angle = direction_angle - 90
        end_angle = direction_angle + 90

        # Create the circular arc using QgsCircularString
        circular_string = QgsCircularString.fromTwoPointsAndCenter(
            start_point, center_point, end_point)

        # Add the circular arc to the rounded line
        rounded_line.addPart(circular_string.toPolyline(), False)

    return rounded_line


line = [QgsPointXY(1,1), QgsPointXY(50, 1.2), QgsPointXY(120,2), ...]
rounded_line = __round(line, 2)

How can I implement the function __round? Now, because of poor docs I cannot find anything helpful.

The black line is what I have (array of vertices). I need somehow to round all the corners (red). All corners must have the same radius (float).

@ComradeChe a little bit yes, but i need the corners to be rounded as a circle, not as any curve that binds two lines. It must be a circle segment with some given radius. It should work the same way the css border-radius works — Alexander Petrushyn, Jul 19 '23 at 09:33
Converting to CompoundCurve geometry after smoothing should solve the problem. — Comrade Che, Jul 19 '23 at 12:11
You're making the invalid assumption that the center of the arc lies on a line perpendicular to the segment through the segment's midpoint. Look at this post for how to find the center. Don't forget to address the special case where the segment is too short to round with the given radius. — Llaves, Jul 22 '23 at 15:39

Taras · Answer 1 · 2023-12-23T11:53:11.277

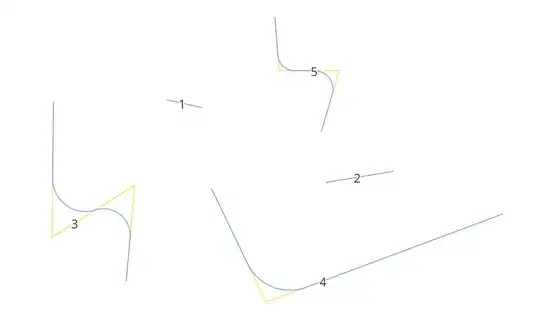
Let's assume there is a polyline layer called 'lines' (five features) with its attribute tables, see the image below.

For this task only features' geometries are required, which is why each of them was converted into a list of QgsPointXYs:

# a list with lists of input points of the QgsPointXY type
input_points = [
    [QgsPointXY(6362950.825627493, 6156755.118187523), QgsPointXY(6362971.421678871, 6156750.437266757)],
    [QgsPointXY(6363045.146180965, 6156706.124550152), QgsPointXY(6363084.699961453, 6156712.677839229)],
    [QgsPointXY(6362883.8446895275, 6156753.833895289), QgsPointXY(6362882.908505374, 6156673.634119468), QgsPointXY(6362931.902142744, 6156704.528196536), QgsPointXY(6362926.909160591, 6156647.733024552)],
    [QgsPointXY(6362977.463104884, 6156702.343766843), QgsPointXY(6363009.605427489, 6156635.250569173), QgsPointXY(6363149.4089277545, 6156687.364820387)],
    [QgsPointXY(6363014.910471025, 6156803.763716814), QgsPointXY(6363017.406962101, 6156772.245516976), QgsPointXY(6363052.981959937, 6156772.245516976), QgsPointXY(6363042.371872864, 6156736.358457757)]
    ]

Further, it is shown as input_points = [...].

A list with QgsPointXYs can be easily converted back to a QgsGeometry using the fromPolylineXY() method of the QgsGeometry class.

The CRS of this data set is the EPSG:5348.

Perhaps you will find one of these solutions for smoothing corners in polylines suitable for you. All the output are of the LineString geometry type.

Please, keep in mind, that:

geometrical dependencies and logical inconsistencies were not handled yet, especially in solutions 1 and 2
the try/except statements were not used
technical issues were not exercised
algorithms were not analysed to increase their performance
improvements and suggestions to this answer are highly welcomed!

Solution 1 : Technique of circles with a specified radius

Proceed with Plugins > Python Console > Show Editor and paste the script below:

# imports
from math import sin, pi
from PyQt5.QtCore import QVariant
from qgis.core import (QgsGeometry, QgsPoint, QgsPointXY, QgsTriangle, QgsLineString, QgsCircularString,\
                       QgsCompoundCurve, QgsFeature, QgsField, QgsVectorLayer, QgsProject, QgsGeometryUtils)
a list with lists of input points of the QgsPointXY type
input_points = [...]
def proper_angle(angle: float) -> float:
    """
    Returns angles only in the range [0, 180] degrees.
    For angles bigger than 180 degrees, gives a value
    of the complementary angle to 360 degrees.
    Parameters:
    ==========
    :param angle: the input angle in radians
    Returns:
    ==========
    :return: angle in radians between 0 and pi
    """
return angle if 0 &lt;= angle &lt;= pi else 2 * pi - angle



def smooth_line_corners(points: list, radius: float) -> QgsLineString:
    """
    It smooths polyline corners using the technique of circles
    with a specified radius placed on the angle bisectors.
    Parameters:
    ==========
    :param points: a list with ordered points for each feature
    :param radius: a radius of a circle applied for smoothing
    Returns:
    ==========
    :return: smoothed feature's geometry of the QgsLineString type
    """
# making lists consisting of three points, starting from the first point and so on
trinities = list(zip(points, points[1:], points[2:]))
# finding angles between three points
angles = [proper_angle(
    QgsGeometryUtils.angleBetweenThreePoints(
        trinity[0].x(), trinity[0].y(),
        trinity[1].x(), trinity[1].y(),
        trinity[2].x(), trinity[2].y()
    )) for trinity in trinities
]
# creating triangles from previous lists
triangles = [QgsTriangle(trinity[0], trinity[1], trinity[2]) for trinity in trinities]
# getting circle centers inscribed into previously created triangles
incenters = [QgsPointXY(triangle.inscribedCircle().center()) for triangle in triangles]
# calculating distances to new circle centers using the provided radius
distances = [radius / sin(angle / 2) for angle in angles]
# finding coordinates of new circle centers that lie on the angles' bisectors
circle_centers = [
    QgsPointXY(QgsGeometryUtils.pointOnLineWithDistance(QgsPoint(values[0]), QgsPoint(values[1]), values[2]))
    for values in list(zip(points[1:-1], incenters, distances))
]
# creating groups consisting of triangles' circle centers and their three vertices
temp1 = {circle: trinities[indx] for indx, circle in enumerate(circle_centers)}

# creating the closest points to the circle centers on two triangles' sides
temp2 = []
for center, vertices in temp1.items():
    poi1 = QgsGeometryUtils.projectPointOnSegment(QgsPoint(center), QgsPoint(vertices[0]), QgsPoint(vertices[1]))
    poi2 = QgsGeometryUtils.projectPointOnSegment(QgsPoint(center), QgsPoint(vertices[1]), QgsPoint(vertices[2]))
    temp2.append(poi1)
    temp2.append(poi2)

# getting only inner points, without the first and the last
temp3 = temp2[1:-1]

# finding out how many sets to consider for calculations
s_num = len(temp3) // 2

# defining how many initial points to consider for calculations, and also skipping the first one
temp4 = points[1:s_num + 1]

# creating groups for comparison distances
pois_on_segment = [temp3[indx:indx + 2] for indx in range(0, len(temp3) - 1, 2)]
temp5 = {poi: pois_on_segment[indx] for indx, poi in enumerate(temp4)}

# comparing distances from the triangle's vertex to two projected points on the same triangle's side
for vertex, proj_pois in temp5.items():
    if (QgsGeometryUtils.sqrDistance2D(QgsPoint(vertex), proj_pois[0]) &gt;
            QgsGeometryUtils.sqrDistance2D(QgsPoint(vertex), proj_pois[1])):
        mid_point = QgsGeometryUtils.midpoint(proj_pois[0], proj_pois[1])
        temp5[vertex] = [mid_point] * len(proj_pois)
        # the approach with a reversed list does not work properly
        # temp5[vertex] = list(reversed(proj_pois))

# flattening a dict to a list
temp6 = []
for k, v in temp5.items():
    temp6.append(k)
    temp6.extend(v)

# projecting first circle center on the first triangle's side
first_proj_poi = QgsGeometryUtils.projectPointOnSegment(QgsPoint(circle_centers[0]), QgsPoint(points[0]),
                                                        QgsPoint(points[1]))
temp6.insert(0, first_proj_poi)

# extending the list with the original pre-last vertex
temp6.extend([QgsPoint(points[-2])])

# projecting last circle center on the last triangle's side
last_proj_poi = QgsGeometryUtils.projectPointOnSegment(QgsPoint(circle_centers[-1]), QgsPoint(points[-1]),
                                                       QgsPoint(points[-2]))
temp6.extend([last_proj_poi])

# replacing the triangle's vertices inside the list with circle centers
points_to_replace = [i + 1 for i in range(0, len(temp6), 3)]
for i, point in enumerate(points_to_replace):
    temp6[point] = QgsPoint(circle_centers[i])

# preparing sets of three points e.g. (projected point on one side, circle center, projected point on another side)
pois_chunks = list(zip(*[iter(temp6)] * 3))

# creating circular strings from the sets of three points with a single arc representing the curve
# from the projected point on one side to projected point on another side with the circle center.
temp7 = []
for chunk in pois_chunks:
    circ_string = QgsCircularString.fromTwoPointsAndCenter(chunk[0], chunk[2], chunk[1], useShortestArc=True)
    temp7.append(circ_string)

# converting each arc to a LineString
temp7 = list(map(lambda curve: curve.curveToLine(), temp7))

# setting up a handler for the output geometry
compound_curve = QgsCompoundCurve()
# adding the first original point
compound_curve.addVertex(QgsPoint(points[0]))
# adding curves with extension of each previous one
for curve in temp7:
    compound_curve.addCurve(curve, extendPrevious=True)
# adding the last original point
compound_curve.addVertex(QgsPoint(points[-1]))

return compound_curve.curveToLine()



creating a polyline layer for the output
output_layer = QgsVectorLayer("LineString?crs={EPSG:5348}&index=yes", "solution1", "memory")
provider = output_layer.dataProvider()
provider.addAttributes([QgsField("id", QVariant.Int)])
output_layer.updateFields()
output_layer.startEditing()
looping over each element in the list
for i, points in enumerate(input_points):
# creating a feature with fields
feat = QgsFeature(output_layer.fields())

# setting new id attribute
feat.setAttribute(&quot;id&quot;, i + 1)

# providing geometry for feature
if len(points) == 2:  # if a straight line
    points = list(map(lambda point: QgsPoint(point), points))
    geom = QgsGeometry.fromPolyline(points)
else: # if a line consists of three and more vertices
    geom = smooth_line_corners(points, 10)
feat.setGeometry(geom)

# adding a feature
output_layer.addFeature(feat)


output_layer.endEditCommand()
output_layer.commitChanges()
adding output layer to the canvas
QgsProject.instance().addMapLayer(output_layer)

Change the input radius in this line smooth_line_corners(points, 10), press Run script and get the output that will look like this:

Solution 2 : Technique of the Inscribed Circles into Triangles

For example, there is a polyline with five points (A, B, C, D, E), see the image below. The resulting smoothed line (pinkish) is simply a polyline composed of (I) straight segments (connections either between the first/last point and projected circle centers or only between projected circle centers on two sides of the triangular, that are segments of the original polyline) and (II) curved lines (arcs created of circle centers and its projections on two sides of the triangular).

This approach also takes into account cases when the projected circle center of the next circle lies closer to the original vertex than the projected circle center of the previous circle. In such circumstances, the implication of a middle point between those two projected points will be considered, see the result below (most left polyline has such a condition).

Proceed with Plugins > Python Console > Show Editor and paste the script below:

# imports
from PyQt5.QtCore import QVariant
from qgis.core import (QgsGeometry, QgsPoint, QgsPointXY, QgsTriangle, QgsLineString, QgsCircularString,\
                       QgsCompoundCurve, QgsFeature, QgsField, QgsVectorLayer, QgsProject, QgsGeometryUtils)
a list with lists of input points of the QgsPointXY type
input_points = [...]
def smooth_line_corners(points: list) -> QgsLineString:
    """
    It smooths polyline corners using the technique of inscribed circles.
    Parameters:
    ==========
    :param points: a list with ordered points for each feature
    Returns:
    ==========
    :return: smoothed feature's geometry of the QgsLineString type
    """
# making lists consisting of three points, starting from the first point and so on
trinities = list(zip(points, points[1:], points[2:]))
# creating triangles from previous lists
triangles = [QgsTriangle(trinity[0], trinity[1], trinity[2]) for trinity in trinities]
# getting circle centers inscribed into previously created triangles
circle_centers = [QgsPointXY(triangle.inscribedCircle().center()) for triangle in triangles]

# creating groups consisting of triangles' inscribed circle centers and their three vertices
temp1 = {circle: trinities[indx] for indx, circle in enumerate(circle_centers)}

# creating the closest points to the circle centers on two triangles' sides
temp2 = []
for center, vertices in temp1.items():
    poi1 = QgsGeometryUtils.projectPointOnSegment(QgsPoint(center), QgsPoint(vertices[0]), QgsPoint(vertices[1]))
    poi2 = QgsGeometryUtils.projectPointOnSegment(QgsPoint(center), QgsPoint(vertices[1]), QgsPoint(vertices[2]))
    temp2.append(poi1)
    temp2.append(poi2)

# getting only inner points, without the first and the last
temp3 = temp2[1:-1]

# finding out how many sets to consider for calculations
s_num = len(temp3) // 2

# defining how many initial points to consider for calculations, and also skipping the first one
temp4 = points[1:s_num + 1]

# creating groups for comparison distances
pois_on_segment = [temp3[indx:indx + 2] for indx in range(0, len(temp3) - 1, 2)]
temp5 = {poi: pois_on_segment[indx] for indx, poi in enumerate(temp4)}

# comparing distances from the triangle's vertex to two projected points on the same triangle's side
for vertex, proj_pois in temp5.items():
    if (QgsGeometryUtils.sqrDistance2D(QgsPoint(vertex), proj_pois[0]) &gt;
            QgsGeometryUtils.sqrDistance2D(QgsPoint(vertex), proj_pois[1])):
        mid_point = QgsGeometryUtils.midpoint(proj_pois[0], proj_pois[1])
        temp5[vertex] = [mid_point] * len(proj_pois)
        # the approach with a reversed list does not work properly
        # temp5[vertex] = list(reversed(proj_pois))

# flattening a dict to a list
temp6 = []
for k, v in temp5.items():
    temp6.append(k)
    temp6.extend(v)

# projecting first circle center on the first triangle's side
first_proj_poi = QgsGeometryUtils.projectPointOnSegment(QgsPoint(circle_centers[0]), QgsPoint(points[0]),
                                                        QgsPoint(points[1]))
temp6.insert(0, first_proj_poi)

# extending the list with the original pre-last vertex
temp6.extend([QgsPoint(points[-2])])

# projecting last circle center on the last triangle's side
last_proj_poi = QgsGeometryUtils.projectPointOnSegment(QgsPoint(circle_centers[-1]), QgsPoint(points[-1]),
                                                       QgsPoint(points[-2]))
temp6.extend([last_proj_poi])

# replacing the triangle's vertices inside the list with circle centers
points_to_replace = [i + 1 for i in range(0, len(temp6), 3)]
for i, point in enumerate(points_to_replace):
    temp6[point] = QgsPoint(circle_centers[i])

# preparing sets of three points e.g. (projected point on one side, circle center, projected point on another side)
pois_chunks = list(zip(*[iter(temp6)] * 3))

# creating circular strings from the sets of three points with a single arc representing the curve
# from the projected point on one side to projected point on another side with the circle center.
temp7 = []
for chunk in pois_chunks:
    circ_string = QgsCircularString.fromTwoPointsAndCenter(chunk[0], chunk[2], chunk[1], useShortestArc=True)
    temp7.append(circ_string)

# converting each arc to a LineString
temp7 = list(map(lambda curve: curve.curveToLine(), temp7))

# setting up a handler for the output geometry
compound_curve = QgsCompoundCurve()
# adding the first original point
compound_curve.addVertex(QgsPoint(points[0]))
# adding curves with extension of each previous one
for curve in temp7:
    compound_curve.addCurve(curve, extendPrevious=True)
# adding the last original point
compound_curve.addVertex(QgsPoint(points[-1]))

return compound_curve.curveToLine()



creating a polyline layer for the output
output_layer = QgsVectorLayer("LineString?crs={EPSG:5348}&index=yes", "solution2", "memory")
provider = output_layer.dataProvider()
provider.addAttributes([QgsField("id", QVariant.Int)])
output_layer.updateFields()
output_layer.startEditing()
looping over each element in the list
for i, points in enumerate(input_points):
# creating a feature with fields
feat = QgsFeature(output_layer.fields())

# setting new id attribute
feat.setAttribute(&quot;id&quot;, i + 1)

# providing geometry for feature
if len(points) == 2:  # if a straight line
    points = list(map(lambda point: QgsPoint(point), points))
    geom = QgsGeometry.fromPolyline(points)
else: # if a line consists of three and more vertices
    geom = smooth_line_corners(points)
feat.setGeometry(geom)

# adding a feature
output_layer.addFeature(feat)


output_layer.endEditCommand()
output_layer.commitChanges()
adding output layer to the canvas
QgsProject.instance().addMapLayer(output_layer)

Press Run script and get the output that will look like this:

Solution 3 : Chaikin's Algorithm

It is implemented via the smooth() method of the QgsGeometry class.

It is based on Chaikin's Algorithm for Curves. The parameters of this function can be adjusted, e.g. iterations=5.

Proceed with Plugins > Python Console > Show Editor and paste the script below:

# imports
from PyQt5.QtCore import QVariant
from qgis.core import QgsProject, QgsFeature, QgsPointXY, QgsLineString, QgsGeometry, QgsField, QgsVectorLayer
a list with lists of input points of the QgsPointXY type
input_points = [...]
def smooth_line_corners(points: list) -> QgsLineString:
    """
    It smooths polyline corners using Chaikin's Algorithm.
    Parameters:
    ==========
    :param points: a list with ordered points for each feature
    Returns:
    ==========
    :return: smoothed feature's geometry of the QgsLineString type
    """
    # creating feature geometry
    geom = QgsGeometry.fromPolylineXY(points)
    # applying the smooth function
    geom_ = geom.smooth(iterations=5, offset=0.25, minimumDistance=-1, maxAngle=180.0)
return geom_.mergeLines()


creating a polyline layer for the output
output_layer = QgsVectorLayer("LineString?crs={EPSG:5348}&index=yes", "solution3", "memory")
provider = output_layer.dataProvider()
provider.addAttributes([QgsField("id", QVariant.Int)])
output_layer.updateFields()
output_layer.startEditing()
looping over each element in the list
for i, points in enumerate(input_points):
    # creating a feature with fields
    feat = QgsFeature(output_layer.fields())
# setting new id attribute
feat.setAttribute(&quot;id&quot;, i + 1)

# providing geometry for feature
geom = smooth_line_corners(points)
feat.setGeometry(geom)

# adding a feature
output_layer.addFeature(feat)


output_layer.endEditCommand()
output_layer.commitChanges()
adding output layer to the canvas
QgsProject.instance().addMapLayer(output_layer)

Press Run script and get the output that will look like this:

See this article for more details: https://observablehq.com/@pamacha/chaikins-algorithm

Solution 4 : Technique of a quadratic Bézier curve

It is implemented via the fromBezierCurve() method of the QgsLineString class.

Note that in this solution controlPoint1 is equal to controlPoint2, and parameter segments=30.

Proceed with Plugins > Python Console > Show Editor and paste the script below:

# imports
from PyQt5.QtCore import QVariant
from qgis.core import (QgsProject, QgsFeature, QgsPoint, QgsPointXY, QgsLineString, QgsGeometry, QgsField,
                       QgsGeometryUtils, QgsCompoundCurve, QgsVectorLayer)
a list with lists of input points of the QgsPointXY type
input_points = [...]
def smooth_line_corners(points: list) -> QgsLineString:
    """
    It smooths polyline corners using a quadratic Bézier curve.
    Parameters:
    ==========
    :param points: a list with ordered points for each feature
    Returns:
    ==========
    :return: smoothed feature's geometry of the QgsLineString type
    """
    # getting only inner points, without the first and the last
    temp1 = points[1:-1]
    # converting each element to QgsPoint type
    temp2 = list(map(lambda point: QgsPoint(point), temp1))
# finding midpoints within inner segments
mid_points = [QgsGeometryUtils.midpoint(pts[0], pts[1]) for pts in zip(temp2[:], temp2[1:])]

# inserting midpoint to odd indexed in the temp2
for indx in range(len(mid_points)):
    temp2.insert(2 * indx + 1, mid_points[indx])

# adding original first vertex
temp2.insert(0, QgsPoint(points[0]))
# extending the list with the original last vertex
temp2.extend([QgsPoint(points[-1])])

# making lists consisting of three points, starting from the first point and so on
trinities = list(zip(temp2[::2], temp2[1::2], temp2[2::2]))

# creating feature geometry
geoms = [QgsGeometry(
    QgsLineString.fromBezierCurve(point[0], point[1], point[1], point[2], segments=30)) for
    point in trinities]
# collecting geometries
geom = QgsGeometry().collectGeometry(geoms)

return geom.mergeLines()


creating a polyline layer for the output
output_layer = QgsVectorLayer("LineString?crs={EPSG:5348}&index=yes", "solution4", "memory")
provider = output_layer.dataProvider()
provider.addAttributes([QgsField("id", QVariant.Int)])
output_layer.updateFields()
output_layer.startEditing()
looping over each element in the list
for i, points in enumerate(input_points):
# creating a feature with fields
feat = QgsFeature(output_layer.fields())

# setting id attribute
feat.setAttribute(&quot;id&quot;, i + 1)

# providing geometry for a feature
if len(points) == 2:  # if a straight line
    points = list(map(lambda point: QgsPoint(point), points))
    geom = QgsGeometry.fromPolyline(points)
else: # if a line consists of three and more vertices
    geom = smooth_line_corners(points)
feat.setGeometry(geom)

# adding a feature
output_layer.addFeature(feat)


output_layer.endEditCommand()
output_layer.commitChanges()
adding output layer to the canvas
QgsProject.instance().addMapLayer(output_layer)

Press Run script and get the output that will look like this:

References:

Thank you for your solution. I also considered Bezier curves and smoothing. But it is impossible to specify the radius of the curve this way (in fact possible, but too tricky). In my case, all the rounding must be parts from circle. They can't be just any curve that binds two lines. It must be a circular rounding. I know how to do it on paper off course, with the help of two perpendicular vectors. But how to implement this function in Qgis and draw the result is for me unimaginable — Alexander Petrushyn, Jul 16 '23 at 20:52

score 4 · Accepted Answer · edited Nov 10 '23 at 13:10

After a research I didn't found a good implementation of what I needed. Bezier curves and QGIS smooth algorithm cannot make the rounding as if its a circle segment. Using these methods you get smoothing, but not rounding.

Here is what I used: (only works on small angles compared to the segment length! Segments don't need to have the same length)

# main function you need
def roundLineVertecies(points: list[QgsPointXY], radius: float) -> QgsGeometry:
    """Round the vertecies of a list of QgsPoint objects.
:param points: List of QgsPoint objects to round, represents the segmented line
:param radius: radius to round.
:returns: QgsGeometry object with rounded vertecies.
&quot;&quot;&quot;

# you need a compound curve object to store the result
compound_curve = QgsCompoundCurve()

# a pointer to the previous point as we iterate through them
last_arc_point = points[0]

for i, point in enumerate(points):
    # continue if its the first point that is not going to be rounded
    if i == 0:
        continue

    # break if its the last point that also doenst need to be rounded, wee just add the point to the curve
    if i == len(points) - 1:
        line = QgsLineString([last_arc_point, point])  # type: ignore
        compound_curve.addCurve(line)
        break

    next_point = points[i + 1]

    # p1 and p2 - see image 1, arc is the curve (line segment connecting them)
    p1, p2, arc = createArc(last_arc_point, point, next_point, radius)

    # draw a line from the end of the curve to the next point
    line = QgsLineString([last_arc_point, p1])

    compound_curve.addCurve(line)
    compound_curve.addCurve(arc)

    # moving the pointer
    last_arc_point = p2

return QgsGeometry(compound_curve)


a helper function to draw a circle segment from 2 points (p1 and p2) on a segment and a center point (r)
def createArc(
    point1: QgsPointXY, point2: QgsPointXY, point3: QgsPointXY, radius: float
) -> Tuple[QgsPointXY, QgsPointXY, QgsCircularString]:
    """Create an arc from three QgsPoint objects.
:param point1: First QgsPoint object.
:param point2: Second QgsPoint object.
:param point3: Third QgsPoint object.
:param radius: Radius of the arc.

:returns: Tuple of QgsPoint objects and QgsCircularString object.
&quot;&quot;&quot;

# finding the circles center coordinates from two points on it and a given radius
point1_close, center, point2_close = arcCenter(point1, point2, point3, radius)

# using Qgis helper to create a curve (circle segment)
arc = QgsCircularString.fromTwoPointsAndCenter(
    QgsPoint(point1_close), QgsPoint(point2_close), QgsPoint(center)
)

return point1_close, point2_close, arc



finally where all the magic happens. Here we find the coordinates of the center and boundaries of the circle segment
def arcCenter(
    point1: QgsPointXY, point2: QgsPointXY, point3: QgsPointXY, radius: float
) -> Tuple[QgsPointXY, QgsPointXY, QgsPointXY]:
    """Get the center of an arc from three QgsPoint objects.
:param point1: First QgsPoint object.
:param point2: Second QgsPoint object.
:param point3: Third QgsPoint object.
:param radius: Radius of the arc.

:returns: QgsPoint object.
&quot;&quot;&quot;

# see image 2
vector1 = QgsVector(point1.x() - point2.x(), point1.y() - point2.y())
vector2 = QgsVector(point3.x() - point2.x(), point3.y() - point2.y())

# normalizing vectors to find the bisector of two lines, because the center of a circle inside the corner will always lies on the bisector (image 3)
vector1_norm = vector1.normalized()
vector2_norm = vector2.normalized()

# finding the bisector (line on which the center lies)
sum = QgsVector(
    vector1_norm.x() + vector2_norm.x(), vector1_norm.y() + vector2_norm.y()
)
sum = sum.normalized()

# finding point on that line that lies on r from the beginning of the corner
sum = QgsVector(sum.x() * radius, sum.y() * radius)

# getting the angle between the bisection and one of the corners edges
alpha = vector2_norm.angle(vector1_norm) / 2

# make sure its between 0 and pi
if sum.y() &lt; 0:
    alpha = -alpha

# result is the center that we were looking for
result = QgsPointXY(point2.x() + sum.x(), point2.y() + sum.y())

# point where the arc begins
result1 = QgsPointXY(
    point2.x() + (vector1_norm.x() * radius / math.tan(alpha)),
    point2.y() + (vector1_norm.y() * radius / math.tan(alpha)),
)

# point where the arc ends
result2 = QgsPointXY(
    point2.x() + (vector2_norm.x() * radius / math.tan(alpha)),
    point2.y() + (vector2_norm.y() * radius / math.tan(alpha)),
)

return result1, result, result2

Image 1:

Image2:

Image 3:

Usage:

segmented_line = [QgsPointXY(0,0), QgsPointXY(10,0.5), QgsPointXY(30,-1), QgsPointXY(100,6)]
result= roundLineVertecies(segmented_line, 10) #type: QgsGeometry

Do not forget to import the Tuple with from typing import Tuple, otherwise you are risking getting such error: NameError: name 'Tuple' is not defined — Taras, Dec 02 '23 at 22:31

Smoothing corners in polyline using PyQGIS

2 Answers2

Please, keep in mind, that:

Solution 1 : Technique of circles with a specified radius

a list with lists of input points of the QgsPointXY type

creating a polyline layer for the output

looping over each element in the list

adding output layer to the canvas

Solution 2 : Technique of the Inscribed Circles into Triangles

a list with lists of input points of the QgsPointXY type

creating a polyline layer for the output

looping over each element in the list

adding output layer to the canvas

Solution 3 : Chaikin's Algorithm

a list with lists of input points of the QgsPointXY type

creating a polyline layer for the output

looping over each element in the list

adding output layer to the canvas

Solution 4 : Technique of a quadratic Bézier curve

a list with lists of input points of the QgsPointXY type

creating a polyline layer for the output

looping over each element in the list

adding output layer to the canvas

a helper function to draw a circle segment from 2 points (p1 and p2) on a segment and a center point (r)

finally where all the magic happens. Here we find the coordinates of the center and boundaries of the circle segment

Linked