Is it a direct projection on 20 faces or on 32 faces?
Can I use PostGIS (with ISEA) to calculate and obtain cell-identifiers?
For hexagons (like Uber H3) or for diamonds (like DGGRID's ISEA4D).
The online literature say nothing:
the Wikipedia short page about ISEA. No clues about algorithm. Citation into the article:
Begin with a Snyder Equal Area projection to a regular icosahedron (...) inscribed in a sphere (...) Then project the hexagon back onto the sphere using the Inverse Snyder Icosahedral equal area projection.the PROJ page for ISEA, used by PostGIS and many other, would be the best source, but it doesn't say much, on the contrary, it creates some confusion by saying "... map projections on polyhedral globes for the dodecahedron and truncated icosahedron". And not shows how to use each polyhedre.
This paper explains how to transform regular icosahedron faces into projection planes and, them, into a Truncated icosahedron of 32 faces... But I am not a good reader of mathematical formalism, nor of Chinese.
NOTES
Clues by illustrations:
- ...
- Step n+1: Lambert azimuthal equal-area projection over each 20 faces of the icosahedron.

- Step n+2: "project back onto the sphere using the Inverse Snyder" each 5 faces to truncate, generating 12 new pentagonal faces. So, the algorithm has a reprojection step?
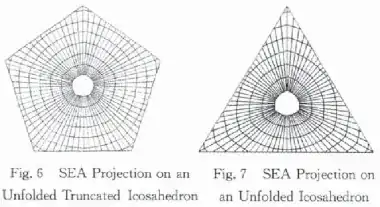
- ...