How to calculate polygon centroids in R (for non-contiguous shapes)

Question

I've spent a little while figuring out the answer to this question. It's not immediately obvious from a Google search, so thought it may useful to post the answer on here. There is also an additional question about non-contiguous polygons.

Instant easy answer: use the command:

centroids <- getSpPPolygonsLabptSlots(polys)

(This was found in the class description of the SpatialPolygonsDataFrame R data class for the overarching spatial package in R, sp)

This seems to do exactly the same thing as

cents <- SpatialPointsDataFrame(coords=cents, data=sids@data, proj4string=CRS("+proj=longlat +ellps=clrk66"))

in the following code, which should be replicable on any R installation (try it!)

#Rcentroids
install.packages("GISTools")
library(GISTools)
sids <- readShapePoly(system.file("shapes/sids.shp", package="maptools")[1], 
                      proj4string=CRS("+proj=longlat +ellps=clrk66"))
class(sids)
plot(sids)
writeSpatialShape(sids, "sids")
cents <- coordinates(sids)
cents <- SpatialPointsDataFrame(coords=cents, data=sids@data, 
                  proj4string=CRS("+proj=longlat +ellps=clrk66"))
points(cents, col = "Blue")
writeSpatialShape(cents, "cents")

centroids <- getSpPPolygonsLabptSlots(sids)
points(centroids, pch = 3, col = "Red")

Where cents (blue) and centroids (red) are identical centroids (this should plot should appear after you've run the code):

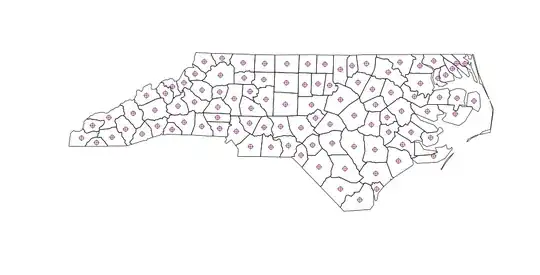
So far so good. But when you calculate polygon centroids in QGIS (menu: Vector | Geometry | Polygon Centroids ), there are slightly different results for non-contiguous polygons:

So this question is 3-things:

1. A quick and easy answer
2. A warning for people using R to calculate centroids for non-contiguous polygons
3. A question about how it should be done in R to properly account for multi-part (non-contiguous) polygons

Answer 1

Firstly, I can't find any documentation that says that coordinates or getSpPPolygonsLabptSlots returns the centre-of-mass centroid. In fact the latter function now shows up as 'Deprecated' and should issue a warning.

What you want for computing the centroid as the centre-of-mass of a feature is the gCentroid function from the rgeos package. Doing help.search("centroid") will have found this.

trueCentroids = gCentroid(sids,byid=TRUE)
plot(sids)
points(coordinates(sids),pch=1)
points(trueCentroids,pch=2)

should show the difference, and be the same as the Qgis centroids.

Answer 2

here is an approach using sf. As I demonstrate, results from sf::st_centroid and rgeos::gCentroid are the same.

library(sf)
library(ggplot2)

# I transform to utm because st_centroid is not recommended for use on long/lat 
nc <- st_read(system.file('shape/nc.shp', package = "sf")) %>% 
  st_transform(32617)

# using rgeos
sp_cent <- gCentroid(as(nc, "Spatial"), byid = TRUE)

# using sf
sf_cent <- st_centroid(nc)

# plot both together to confirm that they are equivalent
ggplot() + 
  geom_sf(data = nc, fill = 'white') +
  geom_sf(data = sp_cent %>% st_as_sf, color = 'blue') + 
  geom_sf(data = sf_cent, color = 'red') 

Answer 3

What I did to overcome this problem is to generate a function which negatively buffers the polygon until it is small enough to expect a convex polygon. The function to use iscentroid(polygon)

#' find the center of mass / furthest away from any boundary
#' 
#' Takes as input a spatial polygon
#' @param pol One or more polygons as input
#' @param ultimate optional Boolean, TRUE = find polygon furthest away from centroid. False = ordinary centroid

require(rgeos)
require(sp)

centroid <- function(pol,ultimate=TRUE,iterations=5,initial_width_step=10){
  if (ultimate){
    new_pol <- pol
    # For every polygon do this:
    for (i in 1:length(pol)){
      width <- -initial_width_step
      area <- gArea(pol[i,])
      centr <- pol[i,]
      wasNull <- FALSE
      for (j in 1:iterations){
        if (!wasNull){ # stop when buffer polygon was alread too small
          centr_new <- gBuffer(centr,width=width)
          # if the buffer has a negative size:
          substract_width <- width/20
          while (is.null(centr_new)){ #gradually decrease the buffer size until it has positive area
            width <- width-substract_width
            centr_new <- gBuffer(centr,width=width)
            wasNull <- TRUE
          }
          # if (!(is.null(centr_new))){
          #   plot(centr_new,add=T)
          # }
          new_area <- gArea(centr_new)
          #linear regression:
          slope <- (new_area-area)/width
          #aiming at quarter of the area for the new polygon
          width <- (area/4-area)/slope
          #preparing for next step:
          area <- new_area
          centr<- centr_new
        }
      }
      #take the biggest polygon in case of multiple polygons:
      d <- disaggregate(centr)
      if (length(d)>1){
        biggest_area <- gArea(d[1,])
        which_pol <- 1                             
        for (k in 2:length(d)){
          if (gArea(d[k,]) > biggest_area){
            biggest_area <- gArea(d[k,])
            which_pol <- k
          }
        }
        centr <- d[which_pol,]
      }
      #add to class polygons:
      new_pol@polygons[[i]] <- remove.holes(new_pol@polygons[[i]])
      new_pol@polygons[[i]]@Polygons[[1]]@coords <- centr@polygons[[1]]@Polygons[[1]]@coords
    }
    centroids <- gCentroid(new_pol,byid=TRUE)
  }else{
    centroids <- gCentroid(pol,byid=TRUE)  
  }  
  return(centroids)
}

#Given an object of class Polygons, returns
#a similar object with no holes


remove.holes <- function(Poly){
  # remove holes
  is.hole <- lapply(Poly@Polygons,function(P)P@hole)
  is.hole <- unlist(is.hole)
  polys <- Poly@Polygons[!is.hole]
  Poly <- Polygons(polys,ID=Poly@ID)
  # remove 'islands'
  max_area <- largest_area(Poly)
  is.sub <- lapply(Poly@Polygons,function(P)P@area<max_area)  
  is.sub <- unlist(is.sub)
  polys <- Poly@Polygons[!is.sub]
  Poly <- Polygons(polys,ID=Poly@ID)
  Poly
}
largest_area <- function(Poly){
  total_polygons <- length(Poly@Polygons)
  max_area <- 0
  for (i in 1:total_polygons){
    max_area <- max(max_area,Poly@Polygons[[i]]@area)
  }
  max_area
}