5

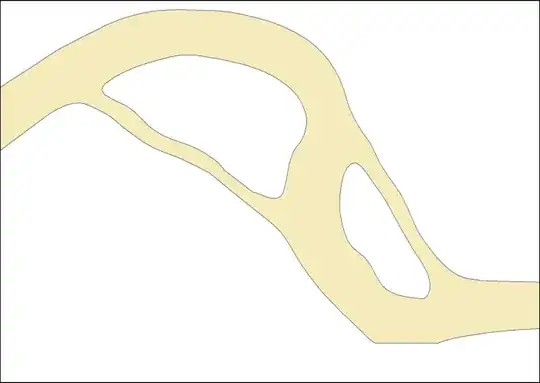
I'm working on deriving the centerline of a polygon, similar to this question or this one, using a different approach. I'm 90% done with the task, but cannot reach the final step. My approach is to calculate a LeastCostPath through the channel center.

In order to do this, I first calculated a surface within the polygon with the distance to the polygon edge (see image 2). In order to get values from 0 - 1 with low values being in the polygon center, I used the following operation:

rastervalueNormalizedInverted = 1-(eucideanDistance/maxRasterValue)

Now I can just calculate the least cost path between the start and end of my polygon and I get a beautiful line without dangles and without the issue of having to specify threshold values (see image 3).

I have the feeling that I'm 90% done at this point. All I have to do now is consider the side channel in polygon, which were not considered by the initial LeastCostPath calculation.

I am completely stuck at this point! I've tried various approaches to get the diverging and converging line for the two side arms seen in the image, with no success. Can anybody provide a clue in which direction I could start looking?

Here are the images to illustrate:

The original Polygon: The original Polygon Normalized, inverted euclidean distance to the polygon edge: Normalized, inverted euclidean distance to the polygon edge Least Cost Path from the start to endpoint of the channel returns a nice line: Least Cost Path from the start to endpoint of the channel returns a nice line

Hornbydd
  • 43,380
  • 5
  • 41
  • 81
Ratnanil
  • 983
  • 8
  • 20

1 Answers1

3

I have spent many hours working on similar problems. I published a paper about it, even. In the Matlab toolbox presented there, I use the shortest path just like you're doing. In my experience, there is no general method that relies on the distance transform that allows resolution of all sub/chute channels. That's not to say one can't be created, but as you've found (and as I've found), it's quite challenging.

I have found the the only way to cope with braiding/anastamosing is to skeletonize your mask. Yes, you end up with many unwanted spurs, but they can be filtered. The skeleton contains the topology you need, albeit with noise. Break it into links and nodes (this is not quite as easy as it sounds if you do it yourself, but I think Arc has some nice tools to help), then you can filter each link based on length, or the change in the distance transform value as you move along the link (e.g. the chute channels' links never approach zero, while a spur almost always reaches the edge of the mask, resulting in a near-zero). Without the topology (i.e. knowing where branchpoints should be), you're stuck. You could develop some threshold-based heuristics for the particular case you show, but it would not be generally applicable.

You might have some luck with watershed algorithms--I never used them but a colleague uses them for centerline delineation (though again, it's only single-thread).

I'll be checking back here to see what you come up with!

Jon
  • 2,894
  • 2
  • 19
  • 35
  • Hey Jon, thank you very much for this excellent reply, and sharing your expertise. I will have a look at your tipps and see if I have to take a step back an use a totally different approach or whether I can actually follow through with the one I started. I'll post any findings here. I'll wait with accepting your answer till then :-) – Ratnanil Mar 08 '18 at 17:30
  • @Ratnanil As you've seen, it's not terribly difficult to get to that 90-95% completion level. The last 5-10% is where things get really tricky and "special-case-y". I won't be offended if you don't accept my answer, for it is not really a good answer toward solving your particular problem. – Jon Mar 08 '18 at 17:40
  • alternative approach: I accept you're answer until I find a concrete, elegant solution (which somehow seems unlikely) – Ratnanil Mar 19 '18 at 07:16