1

Constraints:

Assume -90 < latitude <= 90 and -180 < longitude <= 180.

A bounding box has the form [minLon, minLat, maxLon, maxLat].

Concerns:

  • A solution should be clever to realize that 2 boxes on either side of a boundary should be merged over that boundary.

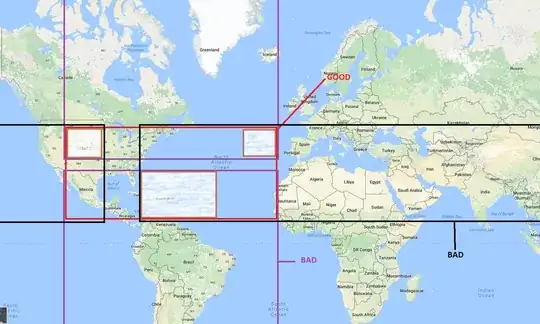
    • Ex: Box_A has left/right longitude bounds of (177, 179), and box_B has (-179, -177). The result should compute (177, -177) and NOT (-177, 177).... may have confused this here, but look at the pictures below to see what I am getting at.

  • If 2 boxes are disjoint, (in my head) there are 4 possible union boxes:

    • Box A is merged with box B on either the left, right, top, or bottom of box A.

  • More than 2 boxes could really slow down a naive approach.

Question:

Is there a python library that will facilitate solving the following problem:

Given a set of bounding boxes {B}, compute a minimum bounding box C such that for all b in {B}, b is contained in C

, and if not, is there at least a library that can compute this result given lat/lon pairs manually extracted from corner points of these boxes?

Clarity:

I am not concerned about what metrics are used to solve the "minimum" box, whether it be area, boundary differences, etc. As long as it is a reasonable and efficient solution.

Visual:

Input:

input

Output (red is good, black and purple are bad):

outputt

EDIT: I just realized the purple box does not actually make sense here on the flat map (read Logan's comment below). I'm going to leave it for now since the principle still applies to the black box at least.

spanishgum
  • 111
  • 4
  • Can you clarify what the single question is? – nmtoken Oct 07 '16 at 19:49
  • Given a set of bounding boxes {B}, how would I compute a bounding box B' such that for all b in {B}, b is contained in B'. I want to do this in python and am not familiar with any gis utilities, but would love to use existing tools (not trying to reinvent the wheel here). – spanishgum Oct 07 '16 at 19:54
  • Can you add your comment clarification to the body of your original post. I still think you are asking more than one question, for example do you just want to know which python libraries to use, or do you want a python solution. At the moment the body has three question marks. You should edit the body so there is only one question. – nmtoken Oct 07 '16 at 20:05
  • Boxes spanning the latitude boundary of the North/South pole shouldn't be a problem, right? It has to stop at those boundaries because "north of the north pole" doesn't wrap to the south pole. – Logan Byers Oct 07 '16 at 20:14
  • Welcome to GIS SE! As a new user please take the [Tour]. Comments are intended for potential answerers to request clarification - any responses you have should be as an [edit] to your question, not as a comment. – Midavalo Oct 07 '16 at 20:42

1 Answers1

0

Use shapely:

from shapely.geometry import box
from shapely.ops import cascaded_union
polygons = [box(i[0],i[1],i[2],i[3]) for i in bbox_list]
unioned = cascaded_union(polygons)
print(unioned.bounds)
sal
  • 392
  • 2
  • 8