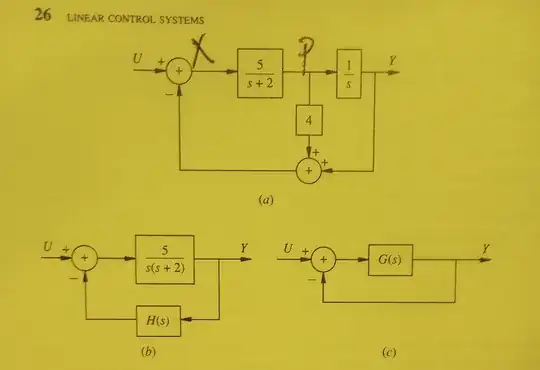
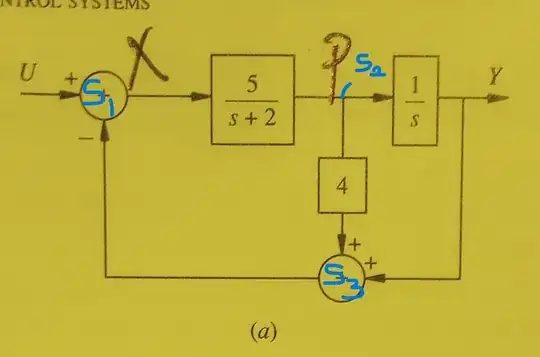
The problem is the one at the top of the page. I was able to reduce the first block diagram into the feedback loop block and I got H(s) = 4s + 1 using the identities in the book. I've spent hours playing with the 5 identities to try and reduce it to the 3rd G(s) block with a feedback loop gain of 1 but I haven't been successful.
The closest I've gotten was in combining the feedback loop block of G and H into one block and trying to find some parallel combination with a gain of 1 but it hasn't worked.
"Linear control systems" Charles Rohrs, James Melsa, Donald Schultz McGraw Hill, 1993