0

Regarding pulse waves specifically. So this should be especially simple.

I see it written that

$$\text{average power} = \text{average current} \times \text{average voltage}$$ which also equals $$ \frac {\text{average voltage} \times\text{average voltage}} {\text{resistance}}$$

This equals $$\frac {(\text{average voltage})^2} {\text{resistance}}$$

But the actual calculation is $$\text{average}(\frac {\text{voltage}^2} {\text{resistance}} )$$.

Marcus Müller
  • 94,373
  • 5
  • 139
  • 252
ramose
  • 107
  • 1
  • 6
  • simply because it's not the average power, as simply trying out would tell you! – Marcus Müller Aug 28 '21 at 13:46
  • so the several places that have written like that are wrong then. ok, I just needed someone to say that. – ramose Aug 28 '21 at 13:53
  • "the average power is the average of the power" is ... not really something you needed someone to say. – Marcus Müller Aug 28 '21 at 13:58
  • no, I needed to hear that a typo is a typo, or both exist as correct in my mind until I hear otherwise. – ramose Aug 28 '21 at 14:10
  • no, you need to learn to use the math you've been given to come to certainty yourself - we can't think for you! – Marcus Müller Aug 28 '21 at 14:12
  • We call it Average Power because if you have a plot of a instantaneous power and you take the average of it you will get the average (real) power. But to get it from a voltage or a current you need to use RMS voltage and RMS current. https://www.analog.com/en/analog-dialogue/raqs/raq-issue-177.html – G36 Aug 28 '21 at 15:00

2 Answers2

1

You can see for yourself that you get different results calculating two different ways. For example, a 10% duty cycle rectangular wave, 0 to V volts, has (square of the average voltage)/resistance = V^2/100R, but the average of (voltage^2/Resistance) is V^2/10R and that's the actual power dissipated averaged over time.

john
  • 127
  • 1
  • 5
1

schematic

simulate this circuit – Schematic created using CircuitLab

Figure 1. A simple periodic waveform stepping from 0 to 1 to 2 V.

Let's assume a 1 Ω load to make it easy.

Average voltage

The average voltage over the period (3 s) is \$ \frac {0 + 1 + 2} 3 = 1 \ \text V \$.

If we use that to calculate the average power in 1 Ω we would get \$ P = \frac {V^2} R = \frac {1^2} 1 = 1 \ \text W \$.

RMS voltage

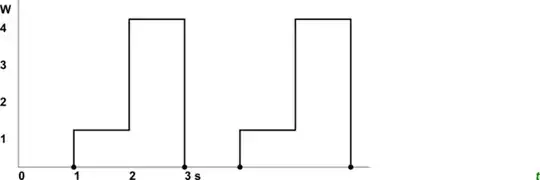
schematic

simulate this circuit

Figure 2. The power waveform for the voltage of Figure 1 into a 1 Ω load.

RMS is the Root of the Mean (average) of the Squares: $$ V_{RMS} = \sqrt {\frac {V_{01}^2 + V_{12}^2 + V_{23}^2} 3} = \sqrt {\frac {0 + 1 + 4} 3} = \sqrt {\frac 5 3 \ \text V} = 1.29 \ \text V $$

If we use that to calculate the average power in 1 Ω we would get \$ P = \frac {V^2} R = \frac {1.29^2} 1 = 1.66 \ \text W \$.

Why the difference?

The higher voltage (2 V) portion of the waveform has a much more significant contribution to the mean power due to the square law. You miss that if you take the average first.

We use the RMS value of a waveform to find that DC voltage that would give the equivalent power, not the average voltage. In the more general case (not using simple rectangular waves as I have here) you would use calculus to integrate the area under the curve of the voltage (or current) squared.

Transistor
  • 175,532
  • 13
  • 190
  • 404
  • so power average actually is NOT current average*voltage average then, and the several places I have seen this are all wrong? We have both shown that ((voltage average)^2)/res is wrong after all. – ramose Aug 28 '21 at 13:52
  • For resistive loads $ P = V_{RMS}\cdot I_{RMS} $. – Transistor Aug 28 '21 at 14:47