Poles and Zeros in Second Order System

Question

I was reading about second order systems and forced/natural responses:

I just want to explain my understanding of what generates the forced and natural responses and want to ask if it is correct:

• The input poles of the input function decide the form of the forced response - step, etc.
• The system poles decide the form of the natural response.
• The amplitude of the forced and natural responses are dictated by ALL of the poles - both input and system.

I don't know if my explanation is correct because if you consider a system that is completely underdamped, that will just continue to oscillate at the output when a step input. In that case, we never even see the form of the forced response at the output (another step) or is the forced response there but just overshadowed by the natural oscillation?

Answer 1

In that case, we never even see the form of the forced response at the output.

We do! The resulting oscillation is actually shifted up by the step part! Notice that the response is always above zero. this is because the step shifted the sinusoid part of the oscillation (which is otherwise symmetric about zero).

is the forced response there but just overshadowed by the natural oscillation?

Yes.

sys = tf([100], [1, 0.1, 100])
step(sys, 10);

Answer 2

The input poles of the input function decide the form of the forced response - step, etc.

If by "form" you mean whether it's constant or damped sinusoid or whatever -- yes. But the input function can have zeros, too, and those do shape the response. For instance, an input function of the form \$X(s) = \frac{a s + b}{s^2}\$ will have a step of amplitude \$a\$ plus a ramp with a slope of \$b\$.

The system poles decide the form of the natural response

Yes.

The amplitude of the forced and natural responses are dictated by ALL of the poles - both input and system.

Poles and zeros

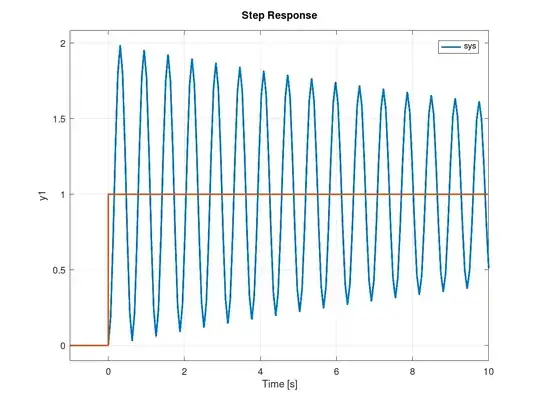
if you consider a system that is completely underdamped, that will just continue to oscillate at the output when a step input.

You will see the input in the output, but a "forever" natural response could be there, too.

But note: if you're overly clever, the "forever" natural response won't be forever. Here's a "low pass" filter with zero damping, $$H = \frac{\omega_0^2}{s^2 + \omega_0^2}$$ where \$\omega_0 = 5(2\pi)\$. It's excited by a finite-duration pulse that someone just happened to arrange to be exactly five cycles of the filter's natural response.

It even has a Laplace transform -- $$X(s) = \frac{1 - e^{- s}}{s}$$

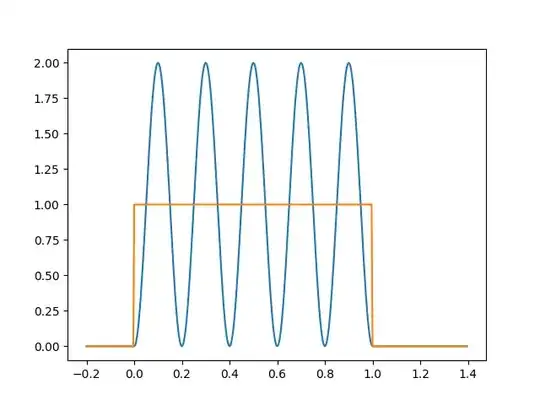
In time-domain terms, the reason that the natural response goes away is because the input signal acts like a step at \$t = 0\$, added to a negative step at \$t = 1\$. Because the "negative step" is an integer number of cycles after the initial step, it's response cancels out the natural response.

In frequency-domain terms, the reason that there's no persistent natural response is because \$X\$ has an infinite number of zeros on the imaginary axis at \$\omega = 2 \pi n\$. One of these falls at \$\omega = 0\$, which is why there's no persisting DC response to the input; another falls at \$\pm\omega_0\$, which is why there's no persisting natural response.

Answer 3

The natural response of a system is the response to initial conditions; the forced response is the response to an applied signal or signals.

If a system has only initial conditions and no input signal, the response is the natural response.

If a system has zero initial conditions and one or more inputs are applied, the response is the forced response.

If a system has initial condition(s) and input signal(s), the response will contain both a natural response and a forced response. In this case the residues at the system poles will have contributions from the natural response and the forced response.