Trapezoidal wave RMS value

Question

I am calculating RMS value of trapezoidal wave.

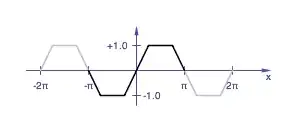
I found its formula like below:

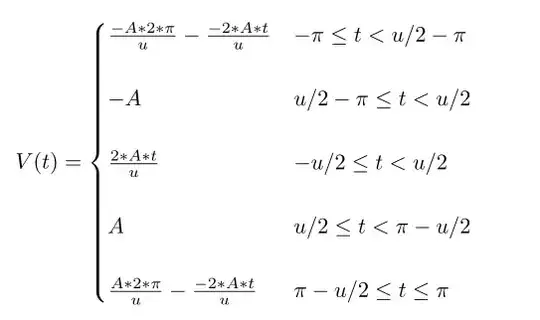
and at last the RMS value formula:

u = 30degree or pi/6 --> especially pi/6

A = 12

When I calculate RMS value by this formula, I got 2 but by matlab, I got 11.314, when I calculate the RMS value by fourier series, I got 8.48 where did I make mistake ?

Here the codes

inputs = -pi:0.0001:pi;
outputs = zeros(1,length(inputs));
u = pi/6;
A = 12;
for i =1:length(inputs)
if inputs(i) <= u/2-pi && inputs(i)>=-pi
    outputs(i) = -2*A*pi/u - 2*A*inputs(i)/u;

elseif inputs(i)>=u/2-pi && inputs(i)<(-u/2)
    outputs(i) = -A;

elseif inputs(i)>=(-u/2) && inputs(i)<=(u/2)
    outputs(i) = 2*A*(inputs(i))/u;

elseif inputs(i)>(u/2) && inputs(i)<=(pi-u/2)
    outputs(i) = A;    


elseif inputs(i)>(pi-u/2) && inputs(i)<(pi)
    outputs(i) = 2*A*(pi - inputs(i))/u;




end


end
mean(outputs)
rms(outputs)
%axis([-10,10,-4pi,4pi]);
plot(inputs,outputs);

Answer 1

The formulas for both the waveform and the RMS calculations have typos. For the waveform's first and last intervals, there is an extra minus in the 2nd terms. The terms should be:

$$\begin{align} &\dfrac{2A}{u}(-\pi-t)\tag{1} \\ &\dfrac{2A}{u}(\pi-t)\tag{2} \end{align}$$

Strangely enough, the way they are written in the integrands is fine, but the result is off in the last integration, it should be the same result as in the first integration:

$$\dfrac{A^2u}{12\pi}\tag{3}$$

Now, if you calculate the sum for the RMS:

$$A\sqrt{2\dfrac{u}{12\pi}+2\dfrac{\pi-u}{2\pi}+\dfrac{u}{6\pi}}=A\sqrt{\dfrac{u}{3\pi}+\dfrac{\pi-u}{\pi}}\tag{4}$$

And if you replace \$u=\pi/6\$ and \$A=12\$:

$$\begin{align} 12\sqrt{\dfrac{\pi}{6}\dfrac{1}{3\pi}+\dfrac{\pi-\dfrac{\pi}{6}}{\pi}}&=12\sqrt{\dfrac{1}{18}+\dfrac{5\pi}{6}\dfrac{1}{\pi}} \\ &=12\sqrt{\dfrac{1}{18}+\dfrac{5}{6}} \\ &=12\sqrt{\dfrac{16}{18}} \\ &=\dfrac{12}{3}\cdot 2^{\frac{3}{2}} \\ &=\dfrac{3\cdot 2^2}{3}\cdot 2^{\frac{3}{2}} \\ &=2^3\cdot 2^{\frac12} \\ &=8\sqrt{2} \tag{5} \end{align}$$

Sorry for the lengthy noobish arithmetic, just wanted to be sure it's clear enough how to reach Spehro Pefhany's result.

Answer 2

where did I make mistake ?

Something is definitely wrong with math formulas. I haven't checked your calculations, but results are very confusing:

1. Why Vrms5 != Vrms1? The wave is symmetric, so they should be equal.

2. How come Vrms5 is negative - in your notation it's the integral of a non-negative function.

3. Why does Vrms approach zero as u approaches zero? Shouldn't Vrms approach A in that case?

Perhaps you should double-check the integrals. They look reasonable and the intent behind them is clear enough, but the result seems wrong.

Answer 3

The formula seems wrong.

You can decide what should be the coorect answer by taking u=0, which gives you a square wave. And for a square wave, the answer is : $$ V_{RMS} = A $$ Thus, the value you got with Matlab seems correct.

The ratio between what you got with Matlab and Fourier series is close to \$\sqrt{2}\$. Maybe you forgot this coefficient ? Are the coefficient of your Fourier series amplitudes or RMS values of the different harmonics ?