I'm trying to calculate the reliability of a system that has proven to be a bit more complicated than I thought. Here is the block diagram for the system:
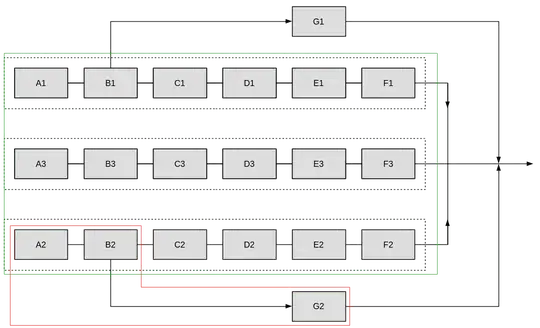
Every single component in this diagram is a Line Replaceable Unit with a mean downtime of 2 hours. If any of A-F fail, that's a failure for the "subsystem" indicated by the dotted line. The entire system will successfully work as long as only 1 of the dotted line, A-F, "subsystems" has failed. Because of the mean downtime of 2 hours, if two of the dotted line subsystems fail within 2 hours of each other, the system fails. This subsystem highlighted in green is not particularly difficult. What's throwing me off is the inclusion of components G1 and G2, routers that fail when either A (UPS) or B (DC power) fails. This makes up the subsystem highlighted in red. The entire system fails if both routers (components G1 and G2) fail, within 2 hours of each other of course.
Basically, I thought that the reliability of the whole system can be calculated with Bayes Theorem which would give the reliability of the system as:
Reliability of green subsystem * probability that G1 and G2 do not fail
PLUS
Reliability of red system * probability that another of the dotted line subsystems does not fail
PLUS
reliability of red system * probability that the other red subsystem does not fail
Unfortunately, I think I'm vastly misunderstanding Bayes Theorem and maybe the system as a whole. Can someone lead me in the right direction to how the inclusion of these G components affects the system reliability? Maybe I just need to re-read up on Bayes Theorem?
Thanks!
****EDIT**** I've simplified the diagram a little bit and I think it moves things along a little bit.
With this diagram (note modified lettering) I was able to determine all possible failure cases, 11 to be exact. The logical expression for whether it passes or not is: ~[(~F & ~G) v (~D & ~C) v (~D & ~E) v (~C & ~E) v (~B & ~C) v (~B & ~D) v (~B & ~A) v (~B & ~F) v (~A & ~C) v (~A & ~E) v (~A & ~G)] which gives the possible failure scenarios: (X, Y)=pair of failed components resulting in a failure.
(F, G) (D, E) (C, E) (C, D) (B, F) (B, D) (B, C) (A, G) (A, E) (A, C) (A, B)
So now my issue is definitely just a matter of Bayes and making sure not to double count.
