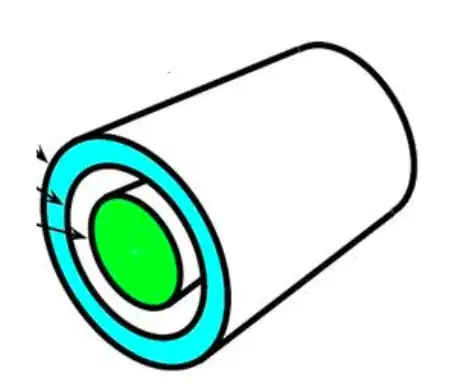
I was wondering how/which area and distance values are calculated for a concentric 2 electrode conductivity sensor (below) when trying to calculate the bulk resistivity of a fluid. The blue is the outer electrode and the green is the inner electrode and the space between is where the fluid would be. Thanks in advance.
-
1If this is homework, can you at least attempt to set up the integral? – jonk Mar 22 '19 at 23:21
-
@jonk its not homework lol. I just got that picture from a google image search. Its a genuine qn for a project i'm working on. – J. Doe Mar 22 '19 at 23:29
-
2I haven't ever thought about this problem before, but this looks to me like you want to create an integral. Suppose $r_1$ is the radius of the inner probe and $r_2$ is the radius of the inner surface of the outer probe. Then you will need to perform an integral that will be something like $\frac{k}{2\pi} \int^{r_2}_{r_1}\frac{1}{r}:\text{d}r$, where $k$ is something I'd need to think more about. I think the solution is going to incorporate something related to $\operatorname{ln}\left(\frac{r_2}{r_1}\right)$. – jonk Mar 22 '19 at 23:40
-
2Hmm. Thinking more I think you can compute the resistivity for a ring as $\rho=R\frac{2\pi}{\operatorname{ln}\frac{r_2}{r_1}}$, with $R$ being the measured resistance. That's just for a ring, though, which I think can be extended to a cylinder. Perhaps I'll pick this up later and double-check my head by using some paper. – jonk Mar 22 '19 at 23:49
2 Answers
Apologies in advance, because I just know that this is not the answer you were hoping for, but truly the correct answer is "you don't".
In practice people determine the cell constant via calibration. See for example:
Page 20 of Conductivity Theory and Practice
Pages 14-15 of the YSI Model 31 Conductivity Bridge Manual
Standard practice is to have a calibrated solution (to be clear, the word "solution" is here used in the sense of "a liquid containing a dissolved solute", not "mathematical answer"...) with a known conductivity then measure it with the cell. Since the cell just measures conductance, you use the (measured) conductance and the (known) conductivity to back-calculate the cell constant.
In theory you could calculate the theoretical cell constant as you suggest, but:
- You've only calculated the perpendicular faces. There are fringing fields that will affect your measurement too. Good luck calculating those. It's not impossible, but you'll need a good finite element modeling tool or something like that.
- Your answer will only be as good as your measurements of the physical dimensions.
- There are some effects (e.g. accumulation of fouling, plating effects) that will affect your cell constant, that will not be accounted for in your equations.
When all is said and done you can do a whole lot of work to calculate a theoretical cell constant that will be only modestly accurate for the reasons outlined above, or you can use a calibrated solution (like the scientists do) and get a much more accurate result. Granted, it's still a whole lot of work, but the end result is decidedly better.
- 2,593
- 9
- 12
-
+1 This is the correct answer, I also remember there were complexities with the measurement frequency and so on when I did conductivity measurement for a company providing medical RO systems. However I expect he can at least get close with the theoretical value to determine dimensions and then calibrate properly. – Spehro Pefhany Mar 23 '19 at 04:49
I think @jonk 99.9% has it in comments above. The resistance of a thin tube of radius r and thickness dr is
\$\rho \text L’ \over \text A \$ (where L' is the length from one contact to the other) or \$\rho dr \over 2\pi \text r \text L \$ (where L is the length of the cylinder)
So the total resistance is the integral from r1 (inner radius) to r2 (outer radius).
R = \$ \int_{r1}^{r2} \frac {\rho} {2\pi \text r \text L} dr \$ = \$ \frac {\rho}{2 \pi \text L} \cdot \ln (\frac {r2}{r1})\$
- 397,265
- 22
- 337
- 893
-
Hey, I'm a bit confused. What's L supposed to represent in the solution? Is it the length of the cylinder? And if that's the case what was 'r' representing when you made A = 2(pi)rL? Thanks. – J. Doe Mar 23 '19 at 10:44
-
1@J.Doe Yes, my L in the solution is the length of the coaxial cylinder. r is the radius of the thin tube .. we’re looking at the resistance from inside to outside with perfectly conductive surfaces on each. But my first L is (was) something different (the thickness dr), so I’ll change it to L’! The rho*L/A is the standard formula for resistance from resistivity, of course. – Spehro Pefhany Mar 23 '19 at 13:43